Корреляционный анализ в excel. пример выполнения корреляционного анализа

Введение

Все чаще объектами статистического анализа становятся не массивы (таблицы) значений, а временные ряды. Такие ряды формируются при наблюдениях за природными процессами и явлениями, изучении социологических или макроэкономических показателей, при промышленном производстве и сбыте продукции. Главное, что отличает временной ряд от других типов данных – это то, что номер (время) наблюдения имеет значение. То есть, важен не только результат измерения, но и тот момент времени, когда оно выполнено. К сожалению, при применении статистических методов на этот нюанс часто не обращают внимания. Однако, именно эта «мелочь» приводит к очень серьезным и нетривиальным следствиям с точки зрения обработки таких сигналов. Самые обычные формулы, описанные во всех учебниках, внезапно отказываются работать. А попытки их применения «в лоб» иногда дают, мягко говоря, весьма неожиданные результаты. Например, статистическая связь между числом пиратов и глобальным потеплением оказывается не просто «значимой», а «практически достоверной». Что удивительно, столкнувшись с такой ситуацией, даже достаточно грамотные исследователи не всегда понимают, где же тут «порылась собака» . Данные вроде бы правильные, математика (как и жена Цезаря) – точно вне подозрений. А результат – ни в какие ворота… А Вы твердо уверены, что всегда правильно оцениваете значимость таких корреляций?

Значения коэффициента корреляции

Охарактеризовать силу корреляционной связи можно прибегнув к шкале Челдока, в которой определенному числовому значению соответствует качественная характеристика.

• 0-0,3 – корреляционная связь очень слабая;
• 0,3-0,5 – слабая;
• 0,5-0,7 – средней силы;
• 0,7-0,9 – высокая;
• 0,9-1 – очень высокая сила корреляции.

Шкала может использоваться и для отрицательной корреляции. В этом случае качественные характеристики заменяются на противоположные.

Можно воспользоваться упрощенной шкалой Челдока, в которой выделяется всего 3 градации силы корреляционной связи:

• очень сильная – показатели ±0,7 — ±1;
• средняя – показатели ±0,3 — ±0,699;
• очень слабая – показатели 0 — ±0,299.

Данный статистический показатель позволяет не только проверить предположение о существовании линейной взаимосвязи между признаками, но и установить ее силу.

История разработки критерия корреляции

Критерий корреляции Пирсона был разработан командой британских ученых во главе с Карлом Пирсоном (1857-1936) в 90-х годах 19-го века, для упрощения анализа ковариации двух случайных величин. Помимо Карла Пирсона над критерием корреляции Пирсона работали также Фрэнсис Эджуорт и Рафаэль Уэлдон.

Для чего используется критерий корреляции Пирсона?

Критерий корреляции Пирсона позволяет определить, какова теснота (или сила) корреляционной связи между двумя показателями, измеренными в количественной шкале. При помощи дополнительных расчетов можно также определить, насколько статистически значима выявленная связь.

Например, при помощи критерия корреляции Пирсона можно ответить на вопрос о наличии связи между температурой тела и содержанием лейкоцитов в крови при острых респираторных инфекциях, между ростом и весом пациента, между содержанием в питьевой воде фтора и заболеваемостью населения кариесом.

Условия и ограничения применения критерия хи-квадрат Пирсона

1. Сопоставляемые показатели должны быть измерены в количественной шкале (например, частота сердечных сокращений, температура тела, содержание лейкоцитов в 1 мл крови, систолическое артериальное давление).
2. Посредством критерия корреляции Пирсона можно определить лишь наличие и силу линейной взаимосвязи между величинами. Прочие характеристики связи, в том числе направление (прямая или обратная), характер изменений (прямолинейный или криволинейный), а также наличие зависимости одной переменной от другой – определяются при помощи регрессионного анализа.
3. Количество сопоставляемых величин должно быть равно двум. В случае анализ взаимосвязи трех и более параметров следует воспользоваться методом факторного анализа.
4. Критерий корреляции Пирсона является параметрическим, в связи с чем условием его применения служит нормальное распределение каждой из сопоставляемых переменных. В случае необходимости корреляционного анализа показателей, распределение которых отличается от нормального, в том числе измеренных в порядковой шкале, следует использовать коэффициент ранговой корреляции Спирмена.
5. Следует четко различать понятия зависимости и корреляции. Зависимость величин обуславливает наличие корреляционной связи между ними, но не наоборот.

Например, рост ребенка зависит от его возраста, то есть чем старше ребенок, тем он выше. Если мы возьмем двух детей разного возраста, то с высокой долей вероятности рост старшего ребенка будет больше, чем у младшего. Данное явление и называется зависимостью, подразумевающей причинно-следственную связь между показателями. Разумеется, между ними имеется и корреляционная связь, означающая, что изменения одного показателя сопровождаются изменениями другого показателя.

В другой ситуации рассмотрим связь роста ребенка и частоты сердечных сокращений (ЧСС). Как известно, обе эти величины напрямую зависят от возраста, поэтому в большинстве случаев дети большего роста (а значит и более старшего возраста) будут иметь меньшие значения ЧСС. То есть, корреляционная связь будет наблюдаться и может иметь достаточно высокую тесноту. Однако, если мы возьмем детей одного возраста, но разного роста, то, скорее всего, ЧСС у них будет различаться несущественно, в связи с чем можно сделать вывод о независимости ЧСС от роста.

Приведенный пример показывает, как важно различать фундаментальные в статистике понятия связи и зависимости показателей для построения верных выводов

Терминология в обработке изображений

Нулевой нормализованной взаимной корреляции (ZNCC)

Для приложений обработки изображений, в которых яркость изображения и шаблона может изменяться в зависимости от освещения и условий экспозиции, изображения могут быть сначала нормализованы. Обычно это делается на каждом этапе путем вычитания среднего и деления на стандартное отклонение . То есть взаимная корреляция шаблона с частичным изображением
т(Икс,у){\ Displaystyle т (х, у)}ж(Икс,у){\ displaystyle f (x, y)}

1п∑Икс,у1σжσт(ж(Икс,у)-μж)(т(Икс,у)-μт){\ displaystyle {\ frac {1} {n}} \ sum _ {x, y} {\ frac {1} {\ sigma _ {f} \ sigma _ {t}}} \ left (f (x, y ) — \ mu _ {f} \ right) \ left (t (x, y) — \ mu _ {t} \ right)}.

где это количество пикселей в и ,
является средним и это стандартное отклонение от .
п{\ displaystyle n}т(Икс,у){\ Displaystyle т (х, у)}ж(Икс,у){\ displaystyle f (x, y)}μж{\ displaystyle \ mu _ {f}}ж{\ displaystyle f}σж{\ displaystyle \ sigma _ {f}}ж{\ displaystyle f}

В терминах функционального анализа это можно рассматривать как скалярное произведение двух нормализованных векторов . То есть, если

F(Икс,у)знак равнож(Икс,у)-μж{\ Displaystyle F (x, y) = f (x, y) — \ mu _ {f}}

и

Т(Икс,у)знак равнот(Икс,у)-μт{\ Displaystyle Т (х, у) = т (х, у) — \ му _ {т}}

тогда указанная сумма равна

⟨F‖F‖,Т‖Т‖⟩{\ displaystyle \ left \ langle {\ frac {F} {\ | F \ |}}, {\ frac {T} {\ | T \ |}} \ right \ rangle}

где — внутренний продукт, а — норма L ² . Затем Коши-Шварц подразумевает, что ZNCC имеет диапазон .
⟨⋅,⋅⟩{\ Displaystyle \ langle \ cdot, \ cdot \ rangle}‖⋅‖{\ displaystyle \ | \ cdot \ |}-1,1{\ displaystyle }

Таким образом, если и являются действительными матрицами, их нормализованная взаимная корреляция равна косинусу угла между единичными векторами и , будучи, таким образом, тогда и только тогда, когда равно умноженному на положительный скаляр.
ж{\ displaystyle f}т{\ displaystyle t}F{\ displaystyle F}Т{\ displaystyle T}1{\ displaystyle 1}F{\ displaystyle F}Т{\ displaystyle T}

Нормализованная корреляция — это один из методов, используемых для сопоставления шаблонов , процесса, используемого для поиска совпадений узора или объекта в изображении. Это также двумерная версия коэффициента корреляции произведения-момента Пирсона .

Нормализованная взаимная корреляция (NCC)

NCC похож на ZNCC с той лишь разницей, что не вычитает локальное среднее значение интенсивности:

1п∑Икс,у1σжσтж(Икс,у)т(Икс,у){\ displaystyle {\ frac {1} {n}} \ sum _ {x, y} {\ frac {1} {\ sigma _ {f} \ sigma _ {t}}} f (x, y) t ( х, у)}

Пример применения метода корреляционного анализа

В Великобритании было предпринято любопытное исследование. Оно посвящено связи курения с раком легких, и проводилось путем корреляционного анализа. Это наблюдение представлено ниже.

Исходные данные для корреляционного анализа

Профессиональная группа	смертность
Фермеры, лесники и рыбаки
Шахтеры и работники карьеров
Производители газа, кокса и химических веществ
Изготовители стекла и керамики
Работники печей, кузнечных, литейных и прокатных станов
Работники электротехники и электроники
Инженерные и смежные профессии
Деревообрабатывающие производства
Кожевенники
Текстильные рабочие
Изготовители рабочей одежды
Работники пищевой, питьевой и табачной промышленности
Производители бумаги и печати
Производители других продуктов
Строители
Художники и декораторы
Водители стационарных двигателей, кранов и т. д.
Рабочие, не включенные в другие места
Работники транспорта и связи
Складские рабочие, кладовщики, упаковщики и работники разливочных машин
Канцелярские работники
Продавцы
Работники службы спорта и отдыха
Администраторы и менеджеры
Профессионалы, технические работники и художники

Начинаем корреляционный анализ. Решение лучше начинать для наглядности с графического метода, для чего построим диаграмму рассеивания (разброса).

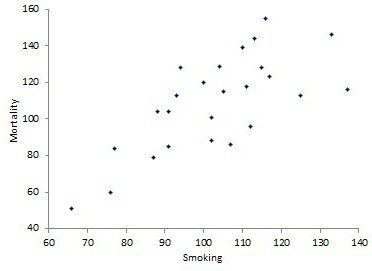
Она демонстрирует прямую связь. Однако на основании только графического метода сделать однозначный вывод сложно. Поэтому продолжим выполнять корреляционный анализ. Пример расчета коэффициента корреляции представлен ниже.

С помощью программных средств (на примере MS Excel будет описано далее) определяем коэффициент корреляции, который составляет 0,716, что означает сильную связь между исследуемыми параметрами. Определим статистическую достоверность полученного значения по соответствующей таблице, для чего нам нужно вычесть из 25 пар значений 2, в результате чего получим 23 и по этой строке в таблице найдем r критическое для p=0,01 (поскольку это медицинские данные, здесь используется более строгая зависимость, в остальных случаях достаточно p=0,05), которое составляет 0,51 для данного корреляционного анализа. Пример продемонстрировал, что r расчетное больше r критического, значение коэффициента корреляции считается статистически достоверным.

Множественная корреляция, её коэффициент

Множественная корреляция — это вероятностная зависимость между одной величиной с
одной стороны, и одновременно несколькими другими ,
с другой стороны.
То есть, в отличие от парной корреляции, при которой
на изменения зависимой (результирующей) переменной влияет одна независимая (объясняющая) переменная,
при множественной корреляции независимых (объясняющих) переменных две или больше.

Цель корреляционного анализа в случае множественной корреляции — установить, есть ли зависимость между
переменными и насколько тесно связаны между собой зависимая переменная, с одной стороны, и независимые
переменные, с другой стороны, и зависят ли друг от друга независимые переменные .

Для того чтобы можно было бы применять модель множественной линейной регрессии, прежде, при анализе
множественной корреляции должны быть установлены следующие факты:

• зависимая переменная тесно зависит от независимых переменных (тесноту связи, как и в случае
  парной корреляции, показывают );
• нет тесной зависимости между независимыми переменными.

Коэффициент множественной корреляции в случае двухфакторной корреляции рассчитывается по следующей формуле:

.

Коэффициенты множественной корреляции между зависимой переменной
и независимыми переменными
записываются в корреляционную матрицу:

Пример 1. Аналитик предприятия решил проверить факторы, которые
влияют на размер заработной платы сотрудников . Предварительно
в качестве объясняющих факторов выбраны: возраст сотрудника ,
стаж работы , оценка теста для приёма
на работу и число подчинённых
сотрудников . Случайно были выбраны
200 сотрудников, данные которых были обобщены. В результате была получена следующая корреляционная матрица:

	1
	-0,27	1
	0,78	-0,63	1
	-0,83	0,47	-0,89	1
	0,65	-0,46	0,17	-0,21	1

Установить, какие переменные можно выбрать как независимые, для того, чтобы далее
можно было бы строить модель множественной регрессии.

Решение.

Корреляционная матрица показывает, что между переменными:

• и — слабая линейная связь: -0,27;
• и — средне тесная положительная линейная связь: 0,78;
• и — тесная отрицательная линейная связь: -0,83;
• и — средне тесная линейная связь: 0,65;
• и — тесная отрицательная линейная связь: -0,89;
• и — слабая линейная связь: 0,17;
• и — слабая линейная связь: -0,21.

Таким образом, не следует включать в число переменных, влияющих на размер заработной
платы возраст сотрудников . Так как
между независимыми переменными и
установлена тесная отрицательная связь,
не включаем в число переменных, влияющих на размер заработной платы стаж работы .
Выбираем в качестве независимых переменных оценку теста для приёма
на работу и число подчинённых
сотрудников .

Чтобы установить тесноту связи между заработной платой сотрудников ,
с одной стороны, и оценкой теста для приёма
на работу и числом подчинённых
сотрудников , с другой стороны,
вычислим коэффициент множественной (двухфакторной) корреляции:

Таким образом, между заработной платой сотрудников, с одной стороны, и
оценкой теста для приёма на работу и числом подчинённых, с другой стороны, существует тесная линейная
связь.

Как показывает пример выше, в исследованиях поведения человека,
как и во многих других направлениях, важно установить, какие факторы из многих действительно влияют на
результат при учете влияния всех остальных факторов

Логнормальное распределение

Логнормальное распределение — это распределение набора значений, чей логарифм нормально распределен. Основание логарифма может быть любым положительным числом за исключением единицы. Как и нормальное распределение, логнормальное распределение играет важную роль для описания многих естественных явлений.

Логарифм показывает степень, в которую должно быть возведено фиксированное число (основание) для получения данного числа. Изобразив логарифмы на графике в виде гистограммы, мы показали, что эти степени приближенно нормально распределены. Логарифмы обычно берутся по основанию 10 или основанию e, трансцендентному числу, приближенно равному 2.718. В функции библиотеки numpy и ее инверсии используется основание e. Выражение log_e также называется натуральным логарифмом, или ln, из-за свойств, делающих его особенно удобным в исчислении.

Логнормальное распределение обычно имеет место в процессах роста, где темп роста не зависит от размера. Этот феномен известен как закон Джибрэта, который был cформулирован в 1931 г. Робертом Джибрэтом, заметившим, что он применим к росту фирм. Поскольку темп роста пропорционален размеру, более крупные фирмы демонстрируют тенденцию расти быстрее, чем фирмы меньшего размера.

Нормальное распределение случается в ситуациях, где много мелких колебаний, или вариаций, носит суммирующий эффект, тогда как логнормальное распределение происходит там, где много мелких вариаций имеет мультипликативный эффект.

С тех пор выяснилось, что закон Джибрэта применим к большому числу ситуаций, включая размеры городов и, согласно обширному математическому ресурсу Wolfram MathWorld, к количеству слов в предложениях шотландского писателя Джорджа Бернарда Шоу.

В остальной части этой серии постов мы будем использовать натуральный логарифм веса спортсменов, чтобы наши данные были приближенно нормально распределены. Мы выберем популяцию спортсменов примерно с одинаковыми типами телосложения, к примеру, олимпийских пловцов.

Линейный коэффициент корреляции Пирсона

Обнаружение взаимосвязей между явлениями – одна из главных задач статистического анализа. На то есть две причины. Первая. Если известно, что один процесс зависит от другого, то на первый можно оказывать влияние через второй. Вторая. Даже если причинно-следственная связь отсутствует, то по изменению одного показателя можно предсказать изменение другого.

Взаимосвязь двух переменных проявляется в совместной вариации: при изменении одного показателя имеет место тенденция изменения другого. Такая взаимосвязь называется корреляцией, а раздел статистики, который занимается взаимосвязями – корреляционный анализ.

Корреляция – это, простыми словами, взаимосвязанное изменение показателей. Она характеризуется направлением, формой и теснотой. Ниже представлены примеры корреляционной связи.

При положительном отклонении X от своей средней, Y также в большинстве случаев отклоняется в положительную сторону от своей средней. Для X меньше среднего, Y, как правило, тоже ниже среднего.

Это прямая или положительная корреляция.

Бывает обратная или отрицательная корреляция, когда положительное отклонение от средней X ассоциируется с отрицательным отклонением от средней Y или наоборот.

Линейность корреляции проявляется в том, что точки расположены вдоль прямой линии. Положительный или отрицательный наклон такой линии определяется направлением взаимосвязи.

Крайне важная характеристика корреляции – теснота. Чем теснее взаимосвязь, тем ближе к прямой точки на диаграмме. Как же ее измерить?

Складывать отклонения каждого показателя от своей средней нет смысла, получим нуль. Похожая проблема встречалась при измерении вариации, а точнее дисперсии. Там эту проблему обходят через возведение каждого отклонения в квадрат.

Квадрат отклонения от средней измеряет вариацию показателя как бы относительно самого себя. Если второй множитель в числителе заменить на отклонение от средней второго показателя, то получится совместная вариация двух переменных, которая называется ковариацией.

Чем больше пар имеют одинаковый знак отклонения от средней, тем больше сумма в числителе (произведение двух отрицательных чисел также дает положительное число).

Критерии и методы

КРИТЕРИЙ СПИРМЕНА

Коэффициент ранговой корреляции Спирмена – это непараметрический метод, который используется с целью статистического изучения связи между явлениями. В этом случае определяется фактическая степень параллелизма между двумя количественными рядами изучаемых признаков и дается оценка тесноты установленной связи с помощью количественно выраженного коэффициента.

Чарльз Эдвард Спирмен

1. История разработки коэффициента ранговой корреляции

Данный критерий был разработан и предложен для проведения корреляционного анализа в 1904 году Чарльзом Эдвардом Спирменом, английским психологом, профессором Лондонского и Честерфилдского университетов.

2. Для чего используется коэффициент Спирмена?

Коэффициент ранговой корреляции Спирмена используется для выявления и оценки тесноты связи между двумя рядами сопоставляемых количественных показателей. В том случае, если ранги показателей, упорядоченных по степени возрастания или убывания, в большинстве случаев совпадают (большему значению одного показателя соответствует большее значение другого показателя — например, при сопоставлении роста пациента и его массы тела), делается вывод о наличии прямой корреляционной связи. Если ранги показателей имеют противоположную направленность (большему значению одного показателя соответствует меньшее значение другого — например, при сопоставлении возраста и частоты сердечных сокращений), то говорят об обратной связи между показателями.

1. Коэффициент корреляции Спирмена обладает следующими свойствами:
2. Коэффициент корреляции может принимать значения от минус единицы до единицы, причем при rs=1 имеет место строго прямая связь, а при rs= -1 – строго обратная связь.
3. Если коэффициент корреляции отрицательный, то имеет место обратная связь, если положительный, то – прямая связь.
4. Если коэффициент корреляции равен нулю, то связь между величинами практически отсутствует.
5. Чем ближе модуль коэффициента корреляции к единице, тем более сильной является связь между измеряемыми величинами.

3. В каких случаях можно использовать коэффициент Спирмена?

В связи с тем, что коэффициент является методом непараметрического анализа, проверка на нормальность распределения не требуется.

Сопоставляемые показатели могут быть измерены как в непрерывной шкале (например, число эритроцитов в 1 мкл крови), так и в порядковой (например, баллы экспертной оценки от 1 до 5).

Эффективность и качество оценки методом Спирмена снижается, если разница между различными значениями какой-либо из измеряемых величин достаточно велика. Не рекомендуется использовать коэффициент Спирмена, если имеет место неравномерное распределение значений измеряемой величины.

4. Как рассчитать коэффициент Спирмена?

Расчет коэффициента ранговой корреляции Спирмена включает следующие этапы:

1. Сопоставить каждому из признаков их порядковый номер (ранг) по возрастанию или убыванию.
2. Определить разности рангов каждой пары сопоставляемых значений (d).
3. Возвести в квадрат каждую разность и суммировать полученные результаты.
4. Вычислить коэффициент корреляции рангов по формуле:

Определить статистическую значимость коэффициента при помощи t-критерия, рассчитанного по следующей формуле:

5. Как интерпретировать значение коэффициента Спирмена?

При использовании коэффициента ранговой корреляции условно оценивают тесноту связи между признаками, считая значения коэффициента меньше 0,3 — признаком слабой тесноты связи; значения более 0,3, но менее 0,7 — признаком умеренной тесноты связи, а значения 0,7 и более — признаком высокой тесноты связи.

Также для оценки тесноты связи может использоваться шкала Чеддока:

_xy
Теснота (сила) корреляционной связи
менее 0.3
слабая
от 0.3 до 0.5
умеренная
от 0.5 до 0.7
заметная
от 0.7 до 0.9
высокая
более 0.9
весьма высокая

Статистическая значимость полученного коэффициента оценивается при помощи t-критерия Стьюдента. Если расчитанное значение t-критерия меньше табличного при заданном числе степеней свободы, статистическая значимость наблюдаемой взаимосвязи — отсутствует. Если больше, то корреляционная связь считается статистически значимой.

9.1.2. Проверка статистических гипотез о связи переменных

Выборочный коэффициент корреляции оценивает подразумеваемую исследователем реальную связь между переменными. Как и в случае оценки среднего значения, нас интересуют два вопроса: (1) Насколько сильна связь между переменными; (2) Насколько надежна наша оценка. Сила связи между переменными по всей генеральной совокупности существует объективно. Если ее измерять корреляцией, то она будет выражаться числом от −1 до 1. Выборочная корреляция этих переменных будет колебаться вокруг истинного показателя силы связи. Трудность состоит в том, что, получив выборочную корреляцию, мы не можем знать, ни насколько она отклоняется от истинного значения, ни даже в какую сторону. В случае корреляции оценка обычно выражается в терминах значимости.

Проделаем небольшое упражнение.

Упражнение 9.1.2(1). Возьмите две симметричные монеты достоинством в один рубль и один евро. Проведите серию четырех подбрасываний пары монет и запишите результаты в виде ​\( (x_1, y_1),\dots,(x_4, y_4) \)​ , полагая

​\( x_i=0 \)​, если рубль выпал цифрой;

​\( x_i=1 \), если рубль выпал гербом;

​\( y_i=0 \), если евро выпал цифрой;

​\( y_i=1 \), если евро выпал гербом.

Подсчитайте коэффициент корреляции Пирсона. Истинная корреляция между результатами двух монет равна, разумеется, нулю. Повторите процедуру несколько раз и убедитесь, что нулевое значение выборочного коэффициента корреляции выпадает примерно один раз из трех. При многократном повторении опыта можно убедиться, что его результат имеет некоторое распределение, симметричное относительно нуля. Это распределение зависит от объема выборки n: чем больше n, тем меньше дисперсия распределения, тем ближе к нулю ее вероятные значения.

В таблице 9.1.2(2) приведены двухсторонние квантили распределения выборочного коэффициента корреляции по Пирсону для ​\( n=10 \)​. Они рассчитаны для выборок, полученных испытаниями двух нормально распределенных случайных величин, теоретическая корреляция между которыми равна нулю. Дихотомический результат подбрасывания монеты не распределен нормально, однако некоторое представление о возможных результатах наших испытаний табличный квантиль все же дает.

Таблица 9.1.2(2) Двусторонние квантили распределения коэффициента Пирсона для n = 10

​\( \alpha \)​	0.05	0.025	0.01	0.005
​\( r_\alpha(10) \)​	0.497	0.576	0.658	0.709

Обычно при исследовании связи переменных статистической гипотезой ​\( H_0 \)​ будет гипотеза об отсутствии связи, т.е. о независимости переменных. Альтернативная гипотеза \( H_1 \)​ (т.е. гипотеза, к которой мы склоняемся, получив большие по модулю значения выборочной корреляции) будет утверждать только наличие связи . Можно оценить значимость относительно данного результата (полученной парной выборки) гипотез о других значениях теоретической корреляции, но это требует некоторых дополнительных усилий (см. подпараграф ). Если истинна гипотеза \( H_0 \)​, то выборочный коэффициент корреляции будет принимать значения, более или менее близкие к нулю. Если выборочная корреляция принимает достаточно большое по модулю значение, которому соответствует значимость, измеряемая маленьким числом, то мы склоняемся к гипотезе \( H_1 \)​ о наличии связи, но без указания точного значения теоретической корреляции.

Можно заметить, что если верна гипотеза  об отсутствии зависимости между случайными величинами, то выборочный коэффициент при \( n=10 \) может принимать тем не менее довольно большие значения, так что уровень значимости 0.05 для принятия гипотезы о зависимости случайных величин требует, чтобы выборочный коэффициент корреляции достигал почти 0.5 (см. ). В связи с этим надо иметь в виду, что даже выборочная корреляция, например 0.6, вполне может согласовываться с истинной корреляцией, равной 0.2 .

Расчет коэффициента корреляции

Разберем расчёт на нескольких образцах. К примеру, есть табличные данные, где по месяцам описаны в отдельных столбцах траты на рекламное продвижение и объём продаж. Исходя из таблицы, будем выяснять уровень зависимости объема продаж от денег, затраченных на рекламное продвижение.

Способ 1: определение корреляции через Мастер функций

КОРРЕЛ – функция, позволяющая реализовать корреляционный анализ. Общий вид – КОРРЕЛ(массив1;массив2). Подробная инструкция:

1. Необходимо произвести выделение ячейки, в которой планируется выводить итог расчета. Нажать «Вставить функцию», находящуюся слева от текстового поля для ввода формулы.

1

1. Открывается «Мастер функций». Здесь необходимо найти КОРРЕЛ, кликнуть на нее, затем на «ОК».

2

1. Открылось окошко аргументов. В строку «Массив1» необходимо ввести координаты интервалы 1-го из значений. В рассматриваемом примере — это столбец «Величина продаж». Нужно просто произвести выделение всех ячеек, которые находятся в этой колонке. В строку «Массив2» аналогично необходимо добавить координаты второй колонки. В рассматриваемом примере — это столбец «Затраты на рекламу».

3

1. После введения всех диапазонов кликаем на кнопку «ОК».

Коэффициент отобразился в той ячейке, которая была указана в начале наших действий. Полученный результат 0,97. Этот показатель отображает высокую зависимость первой величины от второй.

4

Способ 2: вычисление корреляции с помощью Пакета анализа

Существует еще один метод определения корреляции. Здесь используется одна из функций, находящаяся в пакете анализа. Перед ее использованием нужно провести активацию инструмента. Подробная инструкция:

1. Переходим в раздел «Файл».

5

1. Открылось новое окошко, в котором нужно кликнуть на раздел «Параметры».
2. Жмём на «Надстройки».
3. Находим в нижней части элемент «Управление». Здесь необходимо выбрать из контекстного меню «Надстройки Excel» и кликнуть «ОК».

6

1. Открылось специальное окно надстроек. Ставим галочку рядом с элементом «Пакет анализа». Кликаем «ОК».
2. Активация прошла успешно. Теперь переходим в «Данные». Появился блок «Анализ», в котором необходимо кликнуть «Анализ данных».
3. В новом появившемся окошке выбираем элемент «Корреляция» и жмем на «ОК».

7

1. На экране появилось окошко настроек анализа. В строчку «Входной интервал» необходимо ввести диапазон абсолютно всех колонок, принимающих участие в анализе. В рассматриваемом примере — это столбики «Величина продаж» и «Затраты на рекламу». В настройках отображения вывода изначально выставлен параметр «Новый рабочий лист», что означает показ результатов на другом листе. По желанию можно поменять локацию вывода результата. После проведения всех настроек нажимаем на «ОК».

8

Вывелись итоговые показатели. Результат такой же, как и в первом методе – 0,97.

Ближайшая действительная корреляционная матрица

В некоторых приложениях (например, при построении моделей данных только на основе частично наблюдаемых данных) требуется найти «ближайшую» корреляционную матрицу к «приблизительной» корреляционной матрице (например, матрица, которая обычно не имеет полуопределенной положительности из-за того, как она имеет вычислено).

В 2002 году Хайэм формализовал понятие близости с помощью нормы Фробениуса и предоставил метод вычисления ближайшей корреляционной матрицы с использованием алгоритма проекции Дикстры , реализация которого доступна в виде онлайн-веб-API.

Это вызвало интерес к предмету с новыми теоретическими (например, вычисление ближайшей корреляционной матрицы с факторной структурой) и численными (например, использование метода Ньютона для вычисления ближайшей корреляционной матрицы) результатами, полученными в последующие годы.

Характеристики распределений

Основная задача анализа вариационных рядов – это выявление подлинной закономерности распределения, которая достигается увеличением объема исследуемой совокупности при одновременном уменьшении интервала ряда.

Равномерное распределение

Графическое представление Функция плотности равномерного распределения Функция плотности равномерного распределения

Математическое ожидание: Дисперсия:

Нормальное распределение

Графическое представление Плотность распределения Плотность распределения

Математическое ожидание: Дисперсия: Дисперсия: Запись Х ~ N(a>;>Х распределена по нормальному закону с параметрами a и σ.

Примеры решений онлайн: линейная регрессия

Простая выборка

Пример 1. Имеются данные средней выработки на одного рабочего Y (тыс. руб.) и товарооборота X (тыс. руб.) в 20 магазинах за квартал. На основе указанных данных требуется:
1) определить зависимость (коэффициент корреляции) средней выработки на одного рабочего от товарооборота,
2) составить уравнение прямой регрессии этой зависимости.

Пример 2. С целью анализа взаимного влияния зарплаты и текучести рабочей силы на пяти однотипных фирмах с одинаковым числом работников проведены измерения уровня месячной зарплаты Х и числа уволившихся за год рабочих Y:
X 100 150 200 250 300
Y 60 35 20 20 15
Найти линейную регрессию Y на X, выборочный коэффициент корреляции.

Пример 3. Найти выборочные числовые характеристики и выборочное уравнение линейной регрессии $y_x=ax+b$. Построить прямую регрессии и изобразить на плоскости точки $(x,y)$ из таблицы. Вычислить остаточную дисперсию. Проверить адекватность линейной регрессионной модели по коэффициенту детерминации.

Пример 4. Вычислить коэффициенты уравнения регрессии. Определить выборочный коэффициент корреляции между плотностью древесины маньчжурского ясеня и его прочностью. Решая задачу необходимо построить поле корреляции, по виду поля определить вид зависимости, написать общий вид уравнения регрессии Y на Х, определить коэффициенты уравнения регрессии и вычислить коэффициенты корреляции между двумя заданными величинами.

Пример 5. Компанию по прокату автомобилей интересует зависимость между пробегом автомобилей X и стоимостью ежемесячного технического обслуживания Y. Для выяснения характера этой связи было отобрано 15 автомобилей. Постройте график исходных данных и определите по нему характер зависимости. Рассчитайте выборочный коэффициент линейной корреляции Пирсона, проверьте его значимость при 0,05. Постройте уравнение регрессии и дайте интерпретацию полученных результатов.

Корреляционная таблица

Пример 6. Найти выборочное уравнение прямой регрессии Y на X по заданной корреляционной таблице

Пример 7. В таблице 2 приведены данные зависимости потребления Y (усл. ед.) от дохода X (усл. ед.) для некоторых домашних хозяйств.
1. В предположении, что между X и Y существует линейная зависимость, найдите точечные оценки коэффициентов линейной регрессии.
2. Найдите стандартное отклонение $s$ и коэффициент детерминации $R^2$.
3. В предположении нормальности случайной составляющей регрессионной модели проверьте гипотезу об отсутствии линейной зависимости между Y и X.
4. Каково ожидаемое потребление домашнего хозяйства с доходом $x_n=7$ усл. ед.? Найдите доверительный интервал для прогноза.
Дайте интерпретацию полученных результатов. Уровень значимости во всех случаях считать равным 0,05.

Решение об исследовании зависимости (4 страницы)

Пример 8. Распределение 100 новых видов тарифов на сотовую связь всех известных мобильных систем X (ден. ед.) и выручка от них Y (ден.ед.) приводится в таблице:
Необходимо:
1) Вычислить групповые средние и построить эмпирические линии регрессии;
2) Предполагая, что между переменными X и Y существует линейная корреляционная зависимость:
А) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпретацию полученных уравнений;
Б) вычислить коэффициент корреляции, на уровне значимости 0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными X и Y;
В) используя соответствующее уравнение регрессии, оценить среднюю выручку от мобильных систем с 20 новыми видами тарифов.

Коэффициент корреляции

Пример 9. На основании 18 наблюдений установлено, что на 64% вес X кондитерских изделий зависит от их объема Y. Можно ли на уровне значимости 0,05 утверждать, что между X и Y существует зависимость?

Пример 10. Исследование 27 семей по среднедушевому доходу (Х) и сбережениям (Y) дало результаты: $\overline{X}=82$ у.е., $S_x=31$ у.е., $\overline{Y}=39$ у.е., $S_y=29$ у.е., $\overline{XY} =3709$ (у.е.)2. При $\alpha=0,05$ проверить наличие линейной связи между Х и Y. Определить размер сбережений семей, имеющих среднедушевой доход $Х=130$ у.е.

Нужно решить задачи по на тему регрессия и корреляция?

Оставьте заявку сегодня