Округление десятичных дробей: правила, примеры

Округление в Excel в большую сторону при помощи функции ОКРУГЛВВЕРХ

Пользователь может самостоятельно задавать направление для округления. С помощью функции ОКРУГЛВВЕРХ можно убрать лишни цифры или осуществить округление целого числа до того, которое оказывается выше.

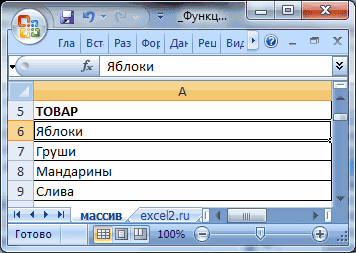
Пример использования этой формулы можно увидеть на этом скриншоте.

6

Основное отличие этой функции от ОКРУГЛ заключается в том, что всегда функция обеспечивает округление с избытком. Если имеются какие-либо разряды числа, округление осуществляется до определенного их количества.

Синтаксис функции ОКРУГЛВВЕРХ

В состав этой функции ходит два аргумента. В целом, функция выглядит следующим образом.

=ОКРУГЛВВЕРХ(76,9;0)

А теперь давайте более подробно разберемся, какие у нее аргументы.

Аргументы функции ОКРУГЛВВЕРХ

Синтаксис у этой функции, как видим, очень простой. Аргументы следующие:1. Число. Это какое-угодно число, для которого требуется округление.

1. Число разрядов. Здесь записывается количество разрядов, которое должно остаться после того, как округление будет осуществлено.

Таким образом, по синтаксису эта формула ничем не отличается от ОКРУГЛ. От модальности числа зависит то, какие именно числа будут сокращаться. Если второй аргумент положительный, то округление оуществляется в правой части от запятой. Если же он отрицательный – то с левой. 

Ошибки округления и модуль decimal

При округлении функцией round(), можно получить следующее:

round(2.65, 1) # = 2.6
round(2.85, 1) # = 2.9

Почему в одном случае округляется вниз, а в другом вверх? При переводе 2.85 в двоичную систему получается число, которое немного больше. Поэтому функция видит не «5», а «>5» и округляет вверх.

Проблему неточного представления чисел отлично иллюстрирует пример:

print (0.1 + 0.1 + 0.1)

0.30000000000000004

Из-за подобных ошибок числа типа «float» нельзя использовать там, где изменения значения на одну тысячную может привести к неверному результату. Решить данную проблему поможет модуль decimal.

decimal — модуль, позволяющий округлять десятичные дроби с почти 100% точностью. Его основной принцип: компьютер должен считать так, как считает человек. Речь идёт не о скорости вычисления, а о точности и отсутствии проблем неправильного представления чисел.

Точные правила округления чисел

При округлении десятичных дробей недостаточно просто отбросить цифры после округляемого разряда. Убедиться в этом можно на таком примере. Если в магазине куплено 2 кг 150 г конфет, то говорят, что приобретено около 2 кг сладостей. Если же вес составляет 2 кг 850 г, то производят округление в большую сторону, то есть около 3 кг. То есть видно, что иногда округляемый разряд изменен. Когда и как это проделывают, смогут ответить точные правила:

1. Если после округляемого разряда следует цифра 0, 1, 2, 3 или 4, то округляемый оставляют неизменным, а все последующие цифры отбрасываются.
2. Если после округляемого разряда следует цифра 5, 6, 7, 8 или 9, то округляемый увеличивают на единицу, а все последующие цифры также отбрасываются.

К примеру, как правильно дробь 7,41 приблизить к единицам. Определяют цифру, которая следует за разрядом. В данном случае это 4. Следовательно, согласно правилу, число 7 оставляют неизменным, а цифры 4 и 1 отбрасывают. То есть получаем 7.

Если округляется дробь 7,62, то после единиц следует цифра 6. Согласно правилу, 7 необходимо увеличить на 1, а цифры 6 и 2 отбросить. То есть в результате получится 8.

Представленные примеры показывают, как округлить десятичные дроби до единиц.

Приближение до целых

Отмечено, что округлять до единиц можно точно так же, как и до целых. Принцип один и тот же. Остановимся подробнее на округлении десятичных дробей до определенного разряда в целой части дроби. Представим пример приближения 756,247 до десятков. В разряде десятых располагается цифра 5. После округляемого разряда следует цифра 6. Следовательно, по правилам необходимо выполнить следующие шаги:

• округление в большую сторону десятков на единицу,
• в разряде единиц цифру 6 заменяют нулем,
• цифры в дробной части числа отбрасываются,
• в результате получают 760.

Обратим внимание на некоторые значения, в которых процесс математического округления до целых по правилам не отображает объективную картину. Если взять дробь 8,499, то, преобразовывая его по правилу, получаем 8

Но по сути это не совсем так. Если поразрядно округлить до целых, то вначале получим 8,5, а затем отбрасываем 5 после запятой, и осуществляем округление в большую сторону.

Получаем 9, что, в принципе, не сосем точно. То есть в таких значениях погрешность существенна. Поэтому оцениваем задачу и, если ситуация позволяет, то лучше использовать значение 8,5.

Приближение до десятых

Как округлить до десятых, до сотых, до тысячных? Операция осуществляется по таким же правилам, как и до целых. Основная задача – правильно определить округляемый разряд и знак, который следует за ним.

К примеру, дробь 6,7864 при доведении:

• до десятых становится равной 6,8,
• до сотых – 6,79,
• если округлить до тысячных, то получают 6,786.

Обратите внимание! Незнание этих правил очень удачно используют маркетологи. В магазинах, наблюдая ценник с указанием числа 5,99, большинством покупателей воспринимается цена, равная 5

В действительности же цена товара практически 6.

Математика учимся округлять числа

Правила округления чисел до десятых

Округление чисел

Для нахождения приближенного значения применяется такое действие как округление чисел.

Слово «округление» говорит само за себя. Округлить число значит сделать его круглым. Круглым называется число, которое оканчивается нулём. Например, следующие числа являются круглыми:

10, 20, 30, 100, 300, 700, 1000

Любое число можно сделать круглым. Процедуру, при которой число делают круглым, называют округлением числá.

Мы уже занимались «округлением» чисел, когда делили большие числа. Напомним, что для этого мы оставляли без изменения цифру, образующую старший разряд, а остальные цифры заменяли нулями. Но это были лишь наброски, которые мы делали для облегчения деления. Своего рода лайфхак. По факту, это даже не являлось округлением чисел. Именно поэтому в начале данного абзаца мы взяли слово округление в кавычки.

На самом деле, суть округления заключается в том, чтобы найти ближайшее значение от исходного. При этом, число может быть округлено до определённого разряда — до разряда десятков, разряда сотен, разряда тысяч.

Рассмотрим простой пример на округление. Дано число 17. Требуется округлить его до разряда десятков.

Не забегая вперёд попробуем понять, что означает «округлить до разряда десятков». Когда говорят округлить число 17, то надо понимать, что от нас требуют найти ближайшее круглое число от числá 17. Причём в ходе этого поиска возможно изменения коснутся и той цифры, которая располагается в разряде десятков числá 17 (т.е цифры 1).

Предстáвим числа от 10 до 20 с помощью следующего рисунка:

На рисунке видно, что для числá 17 ближайшее круглое число это число 20. Значит ответ к задаче таким и будет: «17 приближённо равно 20″

17 ≈ 20

Мы нашли приближённое значение для 17, то есть округлили его до разряда десятков. Видно, что после округления в разряде десятков появилась новая цифра 2.

Попробуем найти приближённое число для числа 12. Для этого снова предстáвим числа от 10 до 20 с помощью рисунка:

На рисунке видно, что ближайшее круглое число для 12 это число 10. Значит ответ к задаче таким и будет: 12 приближённо равно 10

12 ≈ 10

Мы нашли приближённое значение для 12, то есть округлили его до разряда десятков. В этот раз цифра 1, которая стояла в разряде десятков в числе 12, не пострадала от округления. Почему так получилось мы расскажем позже.

Попробуем найти ближайшее число для числá 15. Снова предстáвим числа от 10 до 20 с помощью рисунка:

На рисунке видно, что число 15 одинаково удалено от круглых чисел 10 и 20. Возникает вопрос: которое из этих круглых чисел будет приближённым значением для числа 15? Для таких случаев условились принимать бóльшее число за приближённое. 20 больше чем 10, поэтому приближённое значение для 15 будет число 20

15 ≈ 20

Округлять можно и большие числа. Естественно, для них делать рисунки и изображать числа не представляется возможным. Для них существует свой способ. Например, округлим число 1456 до разряда десятков.

Итак, мы должны округлить 1456 до разряда десятков. Разряд десятков начинается на пятёрке:

Теперь о существовании первых цифр 1 и 4 временно забываем. Остается число 56

Теперь смотрим, какое круглое число находится ближе к числу 56. Очевидно, что ближайшее круглое число для 56 это число 60. Значит заменяем число 56 на число 60

Значит при округлении числа 1456 до разряда десятков полýчим 1460

1456 ≈ 1460

Видно, что после округления числа 1456 до разряда десятков, изменения коснулись и самогó разряда десятков. В новом полученном числе в разряде десятков теперь располагается цифра 6, а не 5.

Округлять числа можно не только до разряда десятков. Округлять число можно до разряда сотен, тысяч, десятков тысяч и так далее.

После того, как станóвится ясно, что округление это ни что иное как поиск ближáйшего числá, можно применять готовые правила, которые значительно облегчают округление чисел.

Правила округления

Коммерческое округление

В Коммерческие туры (не отрицательные числа) выглядит следующим образом :

• Если число в первом десятичном разряде равно 0, 1, 2, 3 или 4, оно округляется в меньшую сторону.
• Если число в первом десятичном разряде — 5, 6, 7, 8 или 9, то оно округляется в большую сторону.

Это правило округления описано в стандарте DIN 1333 . Округление часто уже преподается в начальной школе.

Примеры (округление до двух знаков после запятой):

• 13,3749 … € ≈ 13,37 €
• 13,3750 … € ≈ 13,38 €

Отрицательные числа в зависимости от их величины округлой формы, на 5 , чтобы сказать от нуля ( Engl : от нуля ):

• −13,3749 … € ≈ −13,37 €
• −13,3750 … € ≈ −13,38 €

В Коммерческих турах частично в правовой среде , как гражданские раунды , называемых и г. Б. в о поставщиках государственных услуг пояснил следующее:

Симметричное закругление

Коммерческое и симметричное округление отличаются друг от друга только тем, что число округляется точно посередине между двумя числами с выбранным количеством десятичных цифр.

Симметричные (или геодезическим, математический, искажаются, научный ) округление определяются следующим образом (композиция адаптирована):

1. Если число в первом десятичном разряде равно 0, 1, 2, 3 или 4, оно округляется в меньшую сторону.
2. Если число представляет собой 5 (за которыми следуют другие цифры, которые не равны нулю), 6, 7, 8 или 9 в первом десятичном разряде, оно округляется в большую сторону.
3. Если цифра в первом десятичном разряде, которую следует опустить, представляет собой только 5 (или 5, за которой следуют только нули), она округляется таким образом, чтобы последняя сохраняемая цифра была четной.

Этот тип округления используется в числовой математике , инженерии и технике. Он предусмотрен стандартом IEEE 754 для вычислений с двоичными числами с плавающей запятой в компьютерах. В англоязычной литературе это называется Round to Even или Banker’s Rounding .

Примеры (округление до одного десятичного знака):

• 2,2499 ≈ 2,2 (по правилу 1)
• 2,2501 ≈ 2,3 (по правилу 2)
• 2,2500 ≈ 2,2 (округлено до четного числа согласно правилу 3)
• 2,3500 ≈ 2,4 (округлено до четного числа согласно правилу 3)

Коммерческое округление приводит к небольшим систематическим ошибкам, так как округление на 0,5 происходит в большую сторону, а в меньшую сторону на 0,5 никогда не происходит; это может немного исказить статистику. Математическое округление всегда округляется в большую или меньшую сторону от точной середины между двумя цифрами до следующей четной цифры. В результате среднее значение округляется вверх и вниз примерно так же часто, по крайней мере, если исходные числа являются стохастическими . (Контрпример: если маленькие числа встречаются чаще, чем большие, их можно систематически округлять в меньшую сторону, чем в большую, см . Закон Бенфорда .)

Округление с сохранением суммы

В случае округления с сохранением суммы слагаемые округляются так, чтобы их сумма была равна округленной сумме слагаемых. Может потребоваться округлить некоторые слагаемые от ближайшего округленного значения до противоположного значения.

Важными приложениями являются распределение мест в пропорциональном представительстве и распределение всего НДС в счете-фактуре по его отдельным позициям.

Случай, когда все слагаемые положительные, был тщательно исследован, см. Процедуру распределения мест .

Метод Харе-Нимейера может быть обобщен для слагаемых с обоими знаками : вы округляете все числа до ближайших круглых чисел, и пока сумма слишком велика (или слишком мала), вы выбираете одно из округленных (или округленных) чисел. ) нумерует с наибольшим округление (или самое большое количество округления вниз) и изменяет его округления в направлении , противоположном. Это означает, что сумма изменений минимальна .

Большой толковый словарь

ОКРУГЛЕНИЕ, -я; ср. к Округлить — округлять и Округлиться — округляться. О. форм. О. сумм, капитала, дотаций. О. до двух тысяч. О. дроби. ОКРУГЛЁННЫЙ, -ая, -ое. 1. Имеющий плавно закруглённые линии, очертания; округлый. О-ые верхушки деревьев. О-о лицо. О. почерк. О. жест (плавный, размеренный, лишённый резкости). 2. Стройный, гладкий, законченный (о стиле речи). Выражаться округлёнными фразами. 3. Матем. Принимаемый для удобства без учёта дробных единиц счёта. Округлённо, нареч. Округлённость, -и; ж. О. форм. О. фразы. ОКРУГЛЕТЬ, -ею, -еешь; св. (нсв. круглеть). Разг. =Округлиться (2 зн.). Он значительно округлел. ОКРУГЛИТЬ, -лю, -лишь; округлённый; -лён, -лена, -лено; св. что. 1. (нсв. также круглить). Сделать круглым, придать округлую форму. О. глаза (широко раскрыть их от удивления, страха и т.п.). 2. Выразить в круглых цифрах. О. десятичную дробь. О. счёт. О. стоимость гарнитура. О. итоговую сумму. 3. Разг. Довести до значительных размеров; увеличить. О. капитал. Округлять, -яю, -яешь; нсв. Округляться, -яется; страд. Округление (см.). ОКРУГЛИТЬСЯ, -люсь, -лишься; св. 1. (нсв. также круглиться). Стать круглым, приобрести округлую форму. Глаза округлились у кого-л. (широко раскрылись от страха, удивления и т.п.). 2. Стать полным или более полным; пополнеть, потолстеть. Плечи её округлились. Лицо заметно округлилось. О. к старости. О. во время беременности. Ишь, как округлилась-то на дармовых харчах! 3. только 3 л. Разг. Выразиться в круглых цифрах. Сумма округлилась. Цифра затрат округлилась. Чтобы округлились дотации до ста тысяч, нужно прибавить ещё 30 тысяч. 4. Разг. Достичь значительных размеров; увеличиться. * Уж округлился капитал, В купцы бы надо вскоре (Некрасов). Округляться, -яюсь, -яешься; нсв. Округление (см.). ОКРУГЛО см. Округлый. ОКРУГЛОСТЬ, -и; ж. 1. к Округлый. О. форм. О. букв. О. фраз. 2. обычно мн.: округлости, -ей. Округлые, выпуклые места на теле человека. Всё лицо в округлостях и ямочках. О женской груди. Платье подчёркивало округлости. ОКРУГЛЫЙ, -ая, -ое; округл, -а, -о. 1. Характеризующийся закруглёнными линиями, очертаниями. О. почерк. О-ая кровля башни. О-ые черты лица. О-ые плечи. О. жест (плавный, размеренный, лишённый резкости). 2. Не имеющий резкостей, колкостей, шероховатостей, сглаженный, закруглённый. 3. Выраженный в круглых цифрах. О-ая сумма. О-ые цифры. Округло, нареч. ОКРУГЛЯТЬ см. Округлить. ОКРУГЛЯТЬСЯ см. Округлить и Округлиться.

Правила округления десятичной дроби

Точность — это вежливость королей. А математика, как известно, царица наук, поэтому, чем меньше приближенных значений в ваших решениях, тем лучше.

В повседневной жизни редко можно услышать приближенное значение в ответ на вопросы:

— Который час?

— Какой вес?

— Сколько стоит?

Вряд ли кто-то из нас слышал в ответ 17 часов 27 минут 16 секунд, 1 килограмм 952 грамма или 543 рубля (ладно, с последним бывает).

Округление — это то, с чем мы сталкиваемся каждый день. Поэтому лучше как можно раньше овладеть искусством доводить до приближенного значения. Чтобы без запинки отвечать: половина седьмого; 2 килограмма; 550 рублей.

Число, полученное при округлении, называют приближенным значением данного числа.

Десятичную дробь можно округлить как до целых, так и до разрядов дробной части: десятых, сотых, тысячных и т.д. Чтобы без труда округлить любую десятичную дробь, нужно знать названия всех разрядов.

Если число c < х < d, тогда с — это приближенное значение x с недостатком. А d — это приближенное значение x с избытком.

Чтобы округлить дробную часть десятичной дроби, пользуйтесь следующими правилами:

1. Подчеркните цифру округляемого разряда.
2. Отделите все цифры, стоящие справа.
3. Если справа от цифры, которую нужно округлить, стоит 0, 1, 2, 3 или 4 — цифра остается без изменений. Отбросьте все цифры справа от цифры округляемого разряда.
4. Если справа от цифры округляемого разряда стоит 5, 6, 7, 8 или 9 — к цифре округляемого разряда прибавляем один. Отбросьте все цифры справа.

Приближенное значение записывается после вот такого знака: ≈

Еще одно правило округления, которое нужно запомнить Если при округлении десятичной дроби последней из оставшихся цифр в дробной части оказывается ноль, то его не нужно отбрасывать. Оставшийся ноль показывает, до какого разряда округлено число. Если десятичную дробь округляем до разряда выше единиц (десятков, сотен и т.д.), то дробная часть отбрасывается, а целая часть округляется по правилам округления натуральных чисел.

Второе правило округления

Второе правило округления выглядит следующим образом:

Если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.

Например, округлим число 675 до разряда десятков.

В первую очередь находим сохраняемую цифру. Для этого надо прочитать само задание. В разряде, о котором говорится в задании и находится сохраняемая цифра. В задании сказано: округлить число 675 до разряда десятков.

Видим, что в разряде десятков находится семёрка. Значит сохраняемой цифрой является цифра 7

Теперь находим первую из отбрасываемых цифр. Первой из отбрасываемых цифр является та цифра, которая следует после сохраняемой цифрой. Видим, что первая цифра после семёрки это цифра 5. Значит цифра 5 является первой отбрасываемой цифрой.

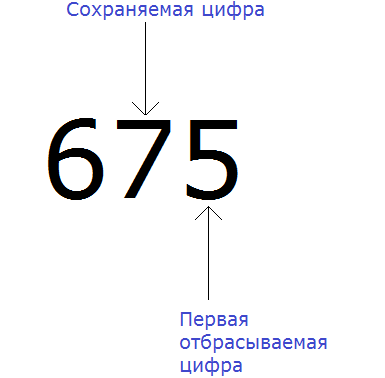
Теперь применяем второе правило округления. Оно говорит, что если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.

У нас первая из отбрасываемых цифр это 5. Значит мы должны увеличить на единицу сохраняемую цифру 7, а всё что следует после неё заменить нулём:

675 ≈ 680

Значит при округлении числа 675 до разряда десятков, получаем приближённое ему число 680.

Теперь попробуем округлить то же самое число 675, но уже до разряда сотен.

Нам требуется округлить число 675 до разряда сотен. Снова ищем сохраняемую цифру. В этот раз сохраняемой цифрой является 6, поскольку мы округляем число до разряда сотен:

Теперь находим первую из отбрасываемых цифр. Первой из отбрасываемых цифр является та цифра, которая следует после сохраняемой цифрой. Видим, что первая цифра после шестёрки это цифра 7. Значит цифра 7 является первой отбрасываемой цифрой:

Теперь применяем второе правило округления. Оно говорит, что если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.

У нас первая из отбрасываемых цифр это 7. Значит мы должны увеличить на единицу сохраняемую цифру 6, а всё что следует после неё заменить нулями:

675 ≈ 700

Значит при округлении числа 675 до разряда сотен, получаем приближённое ему число 700.

Пример 3. Округлить число 9876 до разряда десятков.

Здесь сохраняемая цифра это 7. А первая отбрасываемая цифра это 6. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.

Значит увеличиваем на единицу сохраняемую цифру 7, а всё что располагается после неё заменяем нулём:

9876 ≈ 9880

Пример 4. Округлить число 9876 до разряда сотен.

Здесь сохраняемая цифра это 8. А первая отбрасываемая цифра это 7. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.

Значит увеличиваем на единицу сохраняемую цифру 8, а всё что располагается после неё заменяем нулями:

9876 ≈ 9900

Пример 5. Округлить число 9876 до разряда тысяч.

Здесь сохраняемая цифра это 9. А первая отбрасываемая цифра это 8. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.

Значит увеличиваем на единицу сохраняемую цифру 9, а всё что располагается после неё заменяем нулями:

9876 ≈ 10000

Пример 6. Округлить число 2971 до сотен.

При округлении этого числа до сотен следует быть внимательным, поскольку сохраняемая цифра здесь 9, а первая отбрасываемая цифра это 7. Значит цифра 9 должна увеличиться на единицу. Но дело в том, что после увеличения девятки на единицу получится 10, а это цифра не вместится в разряд сотен нового числа.

В этом случае, в разряде сотен нового числа надо записать 0, а единицу перенести на следующий разряд и сложить с цифрой, которая там находится. Далее заменить все цифры после сохраняемой нулями:

2971 ≈ 3000

Допустимы ли расчеты с работниками в полных рублях?

Начислениезаработной платы округлятьнельзя:

• размер тарифной ставки (оклад) в точной сумме должен быть указан в трудовом договоре (ст. 57 ТК РФ);
• все изменения в оплате труда подписываются двусторонним письменным соглашением (ст. 72 ТК РФ).

Если округлен расчет зарплаты – значит изменен

размер тарифной ставки (оклада) без согласования сторон, а этонарушение.Выплата заработной платы

можетокругляться в большую сторону в пользу работника (Письмо Минздравсоцразвития от 07.12.2005 N 4334-17):

• округление в меньшую сторону ведет к недоплате заработной платы;
• при окончательном расчете с работником (при увольнении) следует выплатить сумму в рублях и копейках;
• порядок округления (в большую сторону) при выплате зарплаты необходимо прописать ЛНА в соответствии со ст. 8 ТК РФ.

Пособия

по нетрудоспособности и в связи с материнством, а также пособия по уходу за ребенком округлятьнельзя (Письмо ФСС от 28.01.2014 N 17-03-11/06-1026).

Округление в компе

Поскольку числа с плавающей запятой занимают только определенную ограниченную область памяти компьютера, точность ограничена системой. После математических операций (таких как умножение) обычно получаются числа, требующие более высокой степени точности. Чтобы по-прежнему можно было отображать результат, его необходимо каким-то образом округлить, чтобы число соответствовало предполагаемому числовому формату (например, IEEE 754 ).

Самая простая схема округления — это обрезка (англ. Truncation or chopping ): ряд определенной точки слева стоять, остальные опущены. Это округляет его до ближайшего возможного числа. Например, если вы округлите до нуля десятичных знаков, a . Этот метод очень быстрый, но он страдает относительно большой ошибкой округления (в примере это так ). Однако клиппинг — незаменимый метод цифровой обработки сигналов . Это единственный метод, который может надежно предотвратить нестабильный предельный цикл из-за ошибок округления в цифровых фильтрах .
10,112знак равно2,7510{\ displaystyle 10 {,} 11_ {2} = 2 {,} 75_ {10}}102знак равно210{\ displaystyle 10_ {2} = 2_ {10}},7510{\ displaystyle 0 {,} 75_ {10}}

Коммерческое округление также используется в качестве дополнительной схемы округления ( округление до ближайшего ). Вы добавляете число, которое нужно округлить, перед округлением, а затем отрезаете. В примере это будет означать, что он будет отрезан . Ошибка здесь только . Однако это округление искажено в лучшую сторону.
,12знак равно,510{\ displaystyle 0 {,} 1_ {2} = 0 {,} 5_ {10}}2,7510+,510знак равно3,25-е10знак равно11,012{\ displaystyle 2 {,} 75_ {10} +0 {,} 5_ {10} = 3 {,} 25_ {10} = 11 {,} 01_ {2}}112знак равно310{\ displaystyle 11_ {2} = 3_ {10}},012знак равно,25-е10{\ displaystyle 0 {,} 01_ {2} = 0 {,} 25_ {10}}

Таким образом, рассматривается математическое округление ( англ. Round-to-ближайшее четное ), которое округляет до следующего четного числа для чисел, оканчивающихся на. Эта процедура округления предусмотрена в стандарте IEEE 754. В качестве альтернативы, также округляется до ближайшего нечетного числа ( англ. Round-to-ближайшее-нечетное ).
…,…510знак равно…,…12{\ Displaystyle \ ldots {,} \ ldots 5_ {10} = \ ldots {,} \ ldots 1_ {2}}

Несмотря на то, что математическое округление хорошо работает в числовом выражении, оно по-прежнему требует полного сложения, потому что в худшем случае бит переноса проходит через все цифры числа. Поэтому он имеет относительно низкую производительность во время выполнения. Готовая таблица с округленными результатами, которую нужно только вызвать, является одним из возможных способов решения этой проблемы.