Перевод в систему си онлайн

Перевод единиц измерения длины

Из прошлых уроков мы знаем, что основные единицы измерения длины это:

• миллиметры;
• сантиметры;
• дециметры;
• метры;
• километры.

Любая величина, которая характеризует длину, может быть переведена из одной единицы измерения в другую.

Кроме того, при решении задач по физике, обязательно нужно соблюдать требования международной системы СИ. То есть если длина дана не в метрах, а в другой единице измерения, то её обязательно нужно перевести в метры, поскольку метр является единицей измерения длины в системе СИ.

Чтобы переводить длину из одной единицы измерения в другую, нужно знать из чего состоит та или иная единица измерения. То есть нужно знать, что к примеру один сантиметр состоит из десяти миллиметров или один километр состоит из тысячи метров.

Покажем на простом примере, как можно рассуждать при переводе длины из одной единицы измерения в другую. Предположим, что имеется 2 метра и нужно перевести их в сантиметры.

Сначала нужно узнать сколько сантиметров содержится в одном метре. В одном метре содержится сто сантиметров:

1 м = 100 см

Если в 1 метре содержится 100 сантиметров, то сколько сантиметров будет содержаться в двух метрах? Ответ напрашивается сам — 200 см. А эти 200 см получаются, если 2 умножить на 100.

Значит, чтобы перевести 2 метра в сантиметры, нужно 2 умножить на 100

2 × 100 = 200 см

Теперь попробуем перевести те же 2 метра в километры. Сначала надо узнать сколько метров содержится в одном километре. В одном километре содержится тысяча метров:

1 км = 1000 м

Если один километр содержит 1000 метров, то километр который содержит только 2 метра будет намного меньше. Чтобы его получить нужно 2  разделить на 1000

2 : 1000 = 0,002 км

Поначалу бывает трудно запомнить, какое действие применять для перевода единиц — умножение или деление. Поэтому на первых порах удобно пользоваться следующей схемой:

Суть данной схемы заключается в том, что при переходе из старшей единицы измерения в младшую применяется умножение. И наоборот, при переходе из младшей единицы измерения в более старшую применяется деление.

Стрелки, которые направлены вниз и вверх указывают на то, что осуществляется переход из старшей единицы измерения в младшую и переход из младшей единицы измерения в более старшую соответственно. В конце стрелки указывается какую операцию применить: умножение или деление.

Например, переведём 3000 метров в километры, пользуясь данной схемой.

Итак, мы должны перейти из метров в километры. Другими словами, перейти из младшей единицы измерения в более старшую (километр старше метра). Смотрим на схему и видим, что стрелка указывающая переход из младших единиц в более старшие, направлена вверх и в конце стрелки указано, что мы должны применить деление:

Теперь нужно узнать, сколько метров содержится в одном километре. В одном километре содержится 1000 метров. А чтобы узнать, сколько километров составляют 3000 таких метров, нужно 3000 разделить на 1000

3000 : 1000 = 3 км

Значит, при переводе 3000 метров в километры, получим 3 километра.

Попробуем перевести те же 3000 метров в дециметры. Здесь мы должны перейти из старших единиц в младшие (дециметр младше метра). Смотрим на схему и видим, что стрелка указывающая переход из старших единиц в младшие, направлена вниз и в конце стрелки указано, что мы должны применить умножение:

Теперь нужно узнать, сколько дециметров в одном метре. В одном метре 10 дециметров.

1 м = 10 дм

А чтобы узнать сколько таких дециметров в трёх тысячах метрах, нужно 3000 умножить на 10

3000 × 10 = 30 000 дм

Значит при переводе 3000 метров в дециметры, получим 30000 дециметров.

Замечания

1. ↑
   In c , h и e — фундаментальные физические константы . Δν _Cs — это универсально воспроизводимая частота, не зависящая от каких-либо правил реализации. N _A — это числовое значение, определяемое по договоренности, которое должно как можно точнее соответствовать коэффициенту пересчета между атомной единицей массы и единицей СИ «грамм». k _B и K _cd — (также произвольно определенные) коэффициенты преобразования между термодинамическими или фотометрическими единицами и единицами MKS.
2. 23 актуальных способа сделать перевод по фото: 5 онлайн сервисов, 11 приложений для телефона и 7 программ для компьютера

   Для производных единиц, которые создаются путем деления, немецкое слово «through» соответствует стандарту — e. Б. «Метр в секунду» (м / с). Однако в разговорной речи слово «профи» является обычным явлением.

3. ↑
   Единицы «Кельвин» и «Кандела» не зависят от скорости света c . Его определение, помимо прочего, зависит от показанной здесь иллюстрации. из единиц «метр» и «килограмм», а они, в свою очередь, из  c . Однако, если значения Кельвина и Канделы полностью сводятся к определяющим константам СИ, то с исключается из расчета .

4. Величина Δ ν _Cs — это частота излучения, испускаемого при переходе между двумя специальными энергетическими уровнями атома цезия-133. Это не свойство материала, а атомарный процесс, на который нельзя повлиять. Однако реализация второго связана с этим процессом. Тем временем были разработаны атомные часы , основанные на других атомах и обеспечивающие еще большую точность . Может быть, поэтому одно изменит второго .

5. Существуют «более прямые» производные единицы, т. Е. ЧАС. определяются меньшим количеством констант, чем базовые единицы: кулон определяется исключительно константой e , для ампера вам также потребуется Δ ν _Cs . Только h и Δ ν _Cs требуются для джоулей и ватт, а c — для килограмма .

6. Для единиц, кратных килограмму,  допускается и обычное использование внесистемной единицы тонна (1 т = 10 3 кг = 1 Мг), из которых такие единицы, как «килотонна» (кт) или «мегатонна» (Мт) могут быть сформированы.

19 thoughts on “Перевод единиц”

Автор, огромное-преогромное спасибо! Для меня математика всю жизнь — это темный лес. А в ваших уроках материал изложен настолько ясно и просто, что все понятно. Хочется учиться дальше. И закрывать эту черную дыру в образовании. Еще раз спасибо и очень жду продолжения уроков.

Здравствуйте админ, при переводе 20 минут в часы, у меня при делении 20 на 60, получился периодическая дробь 0,303030… затем перевел в обыкновенную дробь, получилось 30/99 час, а на самом деле ответ был 3/9. Я не понял период это 30 или 3? Если 3, почему?

Здравствуйте! При делении 20 на 60 должно получиться 0,333… или короче 0,(3)

Затем, если перевести 0,(3) в обыкновенную дробь, должно получится

35 минут и 18 секунд, как будут переведены в часы, но в обыкновенном дробном виде?

Источник

Как использовать конвертер длины

В нашем конвертере собраны самые популярные системы измерения длины:

1. Метрическая — это десятичные числа, кратные метру (метр, километр, дециметр, сантиметр, миллиметр, микрометр, нанометр, ангстрем и т. д).
2. Британо-американская — миля, ярд, фут, дюйм.
3. Старорусская — верста, сажень, аршин, локоть и др.
4. Морская — морская миля, лье, кабельтов Великобритания, США).
5. Астрономические единицы — парсек, световой год.
6. Типографские единицы — пункт, пиксель.

Чтобы сделать перевод из одной системы длины в другую введите число в поле и выберите саму систему. Для ввода дроби можно использовать точку ( . ) Или запятую ( , ). В следующем поле выберите опцию, в которой надо пересчитать. Нажмите кнопку “Перевести”.

Единицы длины, которые часто используют, как в математике, так и в физике:

1 километр (км)	1000 метров (м)
1 метр (м)	100 сантиметров (см)
1 дециметр (дм)	10 сантиметров (см)
1 метр (м)	1000 миллиметров (мм)
1 сантиметр (см)	10 миллиметров (мм)

В Англии и Америке пользуются другими единицами, хотя они не занесены в систему СИ, все равно очень популярны:

1 дюйм (inch)	2,54 сантиметра (см)
1 фут (foot)	30,48 сантиметра (см) или 12 дюймов
1 ярд (yard)	91,44 см или 3 фута
1 миля (mile)	1609,344 метра (м) или 1760 ярдов
1 морская миля (Mn)	1852 метра (м) или 2025,372 ярда

В астрономии используют специальные единицы для определения расстояний:

• астрономическая единица (au) = 149597870700 метров (m)
• 1 световой год = 9,4607 x 1015 метров = 63 241 астрономическая единица (au)
• парсек = 30,8568 трлн км

Ранние системы измерений

В ранних системах мер и системах счисления люди использовали для измерения и сравнения традиционные объекты. Например, считается, что десятичная система появилась в связи с тем, что у нас по десять пальцев на руках и ногах. Наши руки всегда с нами — поэтому с древних времен люди использовали (да и сейчас используют) пальцы для счета. И все же мы не всегда использовали для счета систему с основанием 10, да и метрическая система является относительно новым изобретением. В каждом регионе появлялись свои системы единиц и, хотя у этих систем есть много общего, большинство систем все же настолько разные, что перевод единиц измерения из одной системы в другую всегда был проблемой. Эта проблема становилась все более серьезной по мере развития торговли между разными народами.

Точность первых систем мер и весов напрямую зависела от размеров предметов, которые окружали людей, разрабатывавших эти системы. Понятно, что измерения были неточными, так как «измерительные устройства» не имели точных размеров. Например, в качестве меры длины обычно использовались части тела; масса и объем измерялись с помощью объема и массы семян и других небольших предметов, размеры которых были более-менее одинаковы. Ниже мы подробнее рассмотрим такие единицы.

Меры длины

Локоть и ладонь

В Древнем Египте длина вначале измерялась просто локтями, а позже царскими локтями. Длина локтя определялась как отрезок от локтевого изгиба до конца вытянутого среднего пальца. Таким образом, царский локоть определялся как локоть царствующего фараона. Был создан образцовый локоть, который был доступен широкой публике, чтобы все могли изготовлять свои меры длины. Это, конечно, была произвольная единица, которая изменялась, когда новая царствующая особа занимала престол. В Древнем Вавилоне использовалась похожая система, но с небольшими отличиями.

Локоть делили на более мелкие единицы: ладонь, рука, зерец (фут), and теб (палец), которые были представлены соответственно шириной ладони, руки (с большим пальцем), ступни и пальца. В это же время решили договориться о том, сколько пальцев в ладони (4), в руке (5) и локте (28 в Египте и 30 в Вавилоне). Это было удобнее и точнее, чем каждый раз измерять соотношения.

Меры массы и веса

Меры веса также основывались на параметрах различных предметов. В качестве мер веса выступали семена, зерна, бобы и аналогичные предметы. Классическим примером единицы массы, которая используется до сих пор, является карат. Сейчас каратами измеряют массу драгоценных камней и жемчуга, а когда-то в качестве карата определили вес семян рожкового дерева, иначе называемого кэроб. Дерево культивируется в Средиземноморье, а семена его отличаются постоянством массы, поэтому их удобно было использовать в качестве меры веса и массы. В разных местах в качестве мелких единиц веса использовались разные семена, а бóльшие единицы обычно были кратны более мелким единицам. Археологи часто находят подобные большие меры веса, обычно изготовленные из камня. Они состояли из 60, 100 и иного количества мелких единиц. Поскольку единый стандарт по количеству мелких единиц, а также по их весу отсутствовал, это приводило к конфликтам, когда встречались продавцы и покупатели, которые жили в разных местах.

Меры объема

Первоначально объем также измеряли с помощью небольших предметов. Например, объем горшка или кувшина определяли, наполняя него доверху небольшими предметами относительно стандартного объема — вроде семян. Однако отсутствие стандартизации приводило к тем же проблемам при измерении объема, что и при измерении массы.

Переводим площадь

Разберем принцип, основанный на определении квадратного метра, для пересчета площадей в систему СИ.

Используем принцип единиц в квадрате

Для начала научимся переводить сантиметры в квадрате в квадратные метры. Алгоритм перевода будет состоять из нескольких простых шагов.

Вначале выписываем такое уравнение:

\

Под этим уравнением симметрично записываем еще одно. В правой части нового уравнения каждый метр заменяем количеством входящих в него сантиметров:

\

Затем перемножим правую часть, цифры умножаем на цифры, а сантиметры – на сантиметры. Получим такую запись:

\

В правой части оставим один сантиметр в квадрате. Для этого обе части уравнения разделим на \( \displaystyle 10^{4} \).

\

Теперь можно преобразовать дробь в левой части уравнения, используя свойства степени:

\

Окончательно получим такую запись:

\

Умножая обе части этого выражения на количество сантиметров в квадрате, указанных в условии задачи, получим площадь, переведенную в квадратные метры.

Используем готовые формулы

Повторив описанные выше шаги для нескольких дольных единиц — дециметров и миллиметров, получим такие формулы перевода:

\

\( \displaystyle S_{m} \left(\text{м}^{2} \right) \)  – площадь, выраженная в метрах в квадрате;

\( \displaystyle S_{dm} \left(\text{дм}^{2} \right) \)  – площадь в дециметрах в квадрате;

\( \displaystyle S_{sm} \left(\text{см}^{2} \right) \)  – площадь в квадратных сантиметрах;

\( \displaystyle S_{mm} \left(\text{мм}^{2} \right) \)  – площадь, выраженная в миллиметрах в квадрате;

Эти выражения легко иллюстрировать с помощью квадрата, имеющему длину стороны один метр (рис. 1). Рядом с каждой стороной нужно выписать количество долек, выраженных в меньших единицах измерения и содержащихся в одном метре.

Рис. 1. Квадрат с длиной стороны 1 метр и дольными единицами измерения

Другие единицы длины

Помимо вышеперечисленных, существуют другие единицы для измерения длины. Их использование зависит от вида и места замеров.

Ангстрем (Å) — предназначен для численного выражения очень малых значений длины, сравнимых с размером атомов. Он равняется 10−10 м или одна десятимиллионная миллиметра. Ангстрем назван в честь Андерса Йонаса Ангстрема, шведского физика и астронома, одного из основоположников астрофизики и пионера спектроскопии. Впервые его представили в 1868 году.
Ангстрем часто используется в химии и физике для описания объектов и явлений, происходящих в атомном масштабе. Например, атом водорода имеет радиус 0,37 Å, а длина связи H — H в молекулах H2 немного больше 1 Å. В ангстермах измеряют длину волн излучения, например, видимого, ультрафиолетового, рентгеновского и т.д.Микрометр (мкм или µm) — кратный метру (одна миллионная часть), является единицей длины в системе СИ. 1 мкм = 10−6 м, 1000 мкм равняется 1 мм.

В прошлом эта единица называлась микрон от греческого слова μικρός (мелочь). Название микрона и символ были официальными в 1879-1967 годах.

Морские

Кабельтов — единица расстояния, используемая в навигации. 1 кабельтов = 0,1 морской мили = 608 футов = 185,2 метра.

Морская миля — это единица расстояния, используемая в морской навигации и авиации. Это длина дуги земного меридиана, соответствующая одной угловой минуте большого круга. Фактически, из-за формы земного шара (геоида) длина дуги в 1 угловую минуту изменяется в зависимости от широты, поэтому по соглашению принималась средняя длина 1852 м..

Лье (фр. lieue) старинная французская мера длины. Различали два вида лье:
сухопутное 1л=4,444 км, что соответствует 1/25 градуса меридиана.Земли;
морское 1л=5,556 км, а это 1/20 градуса меридиана.Земли

Астрономические

Астрономическая единица — внесистемная единица расстояния, которая используется в астрономии, составляет ровно 149 597 870 700 м. Это расстояние приблизительно соответствует среднему расстоянию от Земли до Солнца.

Астрономическая единица удобна для определения расстояния между объектами Солнечной системы. Она используется при описании других планетных систем и везде, где есть расстояния сопоставимого порядка, например, в двойных звездных системах.

Парсе́к (pc), русское обозначение (пк) — по научному определению это расстояние до определенной точки, у которой годичный тригонометрический параллакс равняется одной угловой секунде. Отсюда и название — «параллакс» и «секунда».

Простыми словами — парсек это длина катета прямоугольного треугольника, где второй катет равняется одной астрономической единице, а прилежащий угол одной угловой секунде. 

Парсек является официальной единицей системы СИ и его точное значение значение 3.08567758 × 1016 метров.

Несколько интересных фактов:

• от Солнца до самой близкой звезды расстояние в 1,3 парсека;
• чтобы преодолеть 10 пк, лучу света понадобится 32 года 7 месяцев и 6 дней;
• от центра нашей Галактики (ее диаметр 30 кпк) до Солнца приблизительно 8 кпк;
• расстояние до самой близкой к нам туманности Андромеды составит 0,77 Мпк;
• самое близкое к нам скопление галактик Девы находится на расстоянии 18 Мпк.

Световой год — единица расстояния, используемая в астрономии. Он равен расстоянию, которое свет преодолевает в вакууме за один юлианский год (365,25 дня, 31,557,600 секунд). В пересчете на другие единицы: 1 световой год = 0,3066 пк = 63241 I = 9,4607 × 1015 м. Оценки обычно предполагают приблизительное значение ≈ 9,5 трлн км. Конвертер длины поможет в сложных вычислениях.

Типографские

В типографии используются свои меры длины это пиксель и Типогра́фский пункт. Если с пикселем все хорошо знакомы и используют этот термин ежедневно, то что такое Типогра́фский пункт известно, в основном, сотрудникам полиграфии.

Пункт в переводе с немецкого (Punkt) точка. В нем измеряется кегль шрифта. Впервые этот термин использовал французский типограф Пьер-Симон Фурнье в 1737 году. На тот момент он равнялся 0,3473 мм, что составляло 1/12 распространенного в то время шрифта цицеро.

Спустя 33 года, другой типограф из Парижа Франсуа Дидо перевел “пункт” из дюймов в футы, таким образом его размер составил 0,3759 мм. Именно этот параметр стали использовать в Европе, в том числе и в России.

Поскольку в Англии размеры дюйма и фута немного отличались от европейских, в 1878 году Нельсон Хоукс (английский типограф) внес свои корректировки. Согласно его расчетам пункт получился 0,3514 мм. Система Хоукса используется в Америке и Англии.

Для компьютерной верстки используют размер пункта, который предложила компания Adobe и он равен 1/72 дюйма или 0,3528 мм.

Современные меры длины

За долгие годы эталоны измерения длины неоднократно менялись. В настоящее время основной единицей является метр. Название происходит от греческого слова «метрон», что означает «мера»).

Как узнать длину метра

Чтобы это установить, были проведены очень сложные расчеты. Первоначально метр определялся как 1/10 000 четверти меридиана Земли. Затем был изготовлен эталон в виде метрового рельса, который должен был указывать, какая именно длина означает один метр и который хранился в Севре под Парижем. В конце концов, с 1980-х годов длина одного метра рассчитывается на основе расстояния, которое свет проходит в вакууме за 1/299 792 458 с..

Как видите, способы вычисления одного метра довольно сложны, поэтому для нас важнее всего помнить, что метр — это наша основная единица измерения длины и расстояния, которую мы можем преобразовать в меньшие или большие единицы, добавив соответствующие префиксы. Сделать это несложно если использовать конвертер длины.

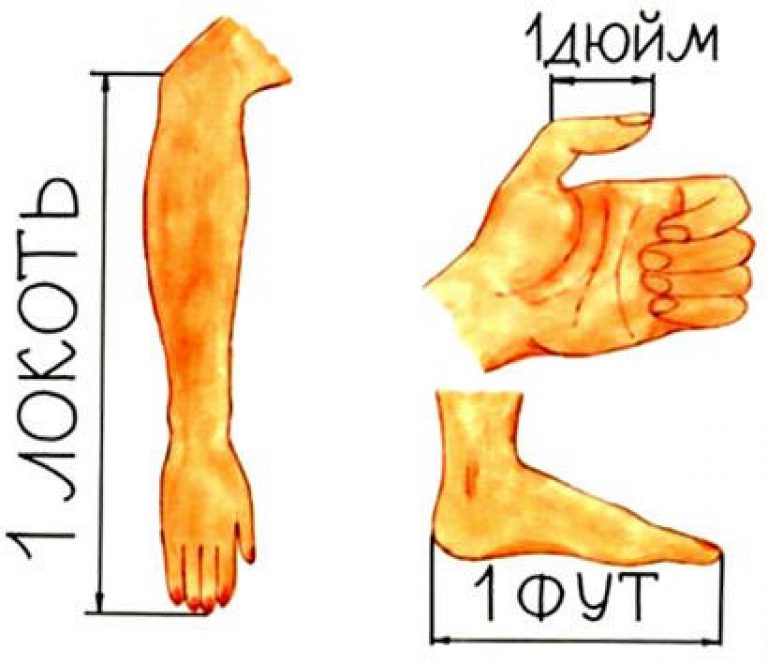
Англосаксонская система

В большинстве стран, включая Россию, используется международная система единиц измерения SI и, соответственно, для длины мы используем метрическую систему. Но есть также страны, такие как Великобритания или США, где используется другая система, так называемая Британо-американская или англосаксонская. Здесь основная единица измерения ярд, а также дюйм, фут, миля, морская миля.

Иногда это может доставить неудобства, например, во время путешествий, если вы не знаете, какие значения им соответствуют. Поэтому стоит иметь под рукой конвертер длины.

Дюйм — единица измерения длины, изначально она соответствовала размеру трех средних зернышек ячменя. Одна из так называемых имперских единиц. В США она является основной, и используется, в частности, в строительстве, медицине, полиции (например, для измерения роста человека), механике и многих других областях.

Фут — древняя единица измерения, относящаяся к средней длине человеческой стопы. В разных странах он был разной длины. Он также изменялся на протяжении веков. В настоящее время наиболее распространенным значением является английский фут = 30,48 см, то есть 1 м = 3,28 футов. Аббревиатура: ft. Чаще всего он составлял 1/2 локтя и делился на 12 дюймов.

Единицы физических величин. Общая информация

Единица физической величины (единица величины, единица, единица измерения) (англ. Measurement unit, unit of measurement, unit) — физическая величина фиксированного размера, которой условно по соглашению присвоено числовое значение, равное 1. С единицей физической величины можно сравнить любую другую величину того же рода и выразить их отношение в виде числа. Применяется для количественного выражения однородных с ней физических величин. Единицы измерения имеют присвоенные им по соглашению наименования и обозначения.Различают основные и производные единицы.

Основные единицы в данной системе единиц устанавливаются для тех физических величин, которые выбраны в качестве основных в соответствующей системе физических величин. Так, Международная система единиц (СИ) основана на Международной системе величин (англ. International System of Quantities, ISQ), в которой основными являются семь величин: длина, масса, время, электрический ток, термодинамическая температура, количество вещества и сила света.Соответственно, в СИ основными единицами являются единицы указанных величин.Размеры основных единиц устанавливаются по соглашению в рамках соответствующей системы единиц и фиксируются либо с помощью эталонов (прототипов), либо путём фиксации численных значений фундаментальных физических постоянных.

Производные единицы определяются через основные путём использования тех связей между физическими величинами, которые установлены в системе физических величин. Существует большое количество различных систем единиц, которые различаются как системами величин, на которых они основаны, так и выбором основных единиц. Государство, как правило, законодательно устанавливает какую-либо систему единиц в качестве предпочтительной или обязательной для использования в стране.

Соотношение единиц измерения

Меры длины 1 км = 1 000 м 1 дм = 10 см = 100 мм 1 м = 10 дм = 100 см 1 см = 10 мм 1 мм = 1 000 мк	Меры площади   1 км2 = 100 га = 10 000 а = 1 000 000 м2 1 га = 100 а = 10 000 м2 1 а = 100 м2 = 10 000 дм2 1 м2 = 100 дм2= 10 000 см2 1 дм2 = 100 см2= 10 000 мм2 1 см2 = 100 мм2 1 мм2 = 0,01 см2
Меры объема 1 м3 = 1 000 дм3 1 дм3= 1 000 см3 1 л = 1 дм31 см3 = 1 000 мм3 1 мм3 = 0,001 см3	Меры веса 1 т = 10 ц = 1 000 кг 1 ц = 100 кг 1 кг = 1 000 г 1 г = 1 000 мг 1 мг = 0,001 г
Меры времени    1 век = 100 лет 1 год = 12 мес = 365 или 366 сут 1 мес = 30 сут или 31 сут (в феврале 28 или 29 сут) 1 неделя = 7 сут 1 сут = 24 ч= 86 400 сек 1 ч = 60 мин = 3 600 сек 1 мин = 60 с 1 сек = 1 000 мсек	Меры давления   1 ат = 1 кГ/см2 = 735,66 мм рт. ст. 1 мм рт. ст. = 1,36 Г/см2
Меры тока   1 ка = 1 000 а 1 а = 1 000 ма 1 ма = 1 000 мка	Меры напряжения и э.д.с.  1 кв. = 1 000 в 1 в = 1 000 мв 1 мв = 1 000 мкв
Меры мощности 1 квт = 1 000 вт 1 вт = 1 000 мвт 1 мвт = 1 000 мквт	Меры сопротивления 1 Мом = 1 000 ком 1 ком = 1 000 ом. 1 ом = 0,001 ком
Меры частоты 1 Мгц = 1 000 кгц 1кгц = 1 000 гц	Меры количества информации 1 байт = 8 бит1 Кб (1 Килобайт) = 210 байт == 1024 байт (~103 байт)1 Мб (1 Мегабайт) = 220 байт = 1024 килобайт (~ 106 байт)1 Гб (1 Гигабайт) = 230 байт = 1024 мегабайт (~ 109 байт)1 Тб (1 Терабайт) = 240 байт = 1024 гигабайт (~ 1012 байт) 1 Пб (1 Петабайт) = 250 байт = 1024 терабайт (~1015 байт)1 Эксабайт = 260 байт = 1024 петабайт (~1018 байт)1 Зеттабайт = 270 байт = 1024 эксабайт (~1021 байт)1 Йоттабайт = 280 байт = 1024 зеттабайт (~ 1024 байт)

Для  единиц измерения информации степени двойки (210, 220 и т.д.) являются точными значениями килобайт, мегабайт, гигабайт. А степени числа 10 (103, 106 и т.п.) — приблизительные значения, округленные в сторону уменьшения. Такое приближение (или округление) вполне допустимо и является общепринятым 

Перевод единиц измерения массы

Из прошлых уроков мы знаем, что основные единицы измерения массы это:

• миллиграммы;
• граммы;
• килограммы;
• центнеры;
• тонны.

Любая величина, которая характеризует массу, может быть переведена из одной единицы измерения в другую.

Кроме того, при решении задач по физике, обязательно нужно соблюдать требования международной системы СИ. То есть если масса дана не в килограммах, а в другой единице измерения, то её обязательно нужно перевести в килограммы, поскольку килограмм является единицей измерения массы в системе СИ.

Чтобы переводить массу из одной единицы измерения в другую, нужно знать из чего состоит та или иная единица измерения. То есть нужно знать, что к примеру один килограмм состоит из тысячи граммов или один центнер состоит из ста килограммов.

Покажем на простом примере, как можно рассуждать при переводе массы из одной единицы измерения в другую. Предположим, что имеется 3 килограмма и нужно перевести их в граммы.

Сначала нужно узнать сколько граммов содержится в одном килограмме. В одном килограмме содержится тысяча граммов:

1 кг = 1000 г

Если в 1 килограмме 1000 граммов, то сколько граммов будут содержаться в трёх таких килограммах? Ответ напрашивается сам — 3000 граммов. А эти 3000 граммов получаются путем умножения 3 на 1000. Значит, чтобы перевести 3 килограмма в граммы, нужно 3 умножить на 1000

3 × 1000 = 3000 г

Теперь попробуем перевести те же 3 килограмма в тонны. Сначала нужно узнать сколько килограммов содержатся в одной тонне. В одной тонне содержится тысяча килограмм:

1 т = 1000 кг

Если одна тонна содержит 1000 килограмм, то тонна которая содержит только 3 килограмма будет намного меньше. Чтобы её получить нужно 3 разделить на 1000

3 : 1000 = 0,003 т

Как и в случае с переводом единиц измерения длины, на первых порах удобно пользоваться следующей схемой:

Данная схема позволит быстро сориентироваться какое действие выполнить для перевода единиц — умножение или деление.

Например, переведём 5000 килограмм в тонны, пользуясь данной схемой.

Итак, мы должны перейти из килограммов в тонны. Другими словами, перейти из младшей единицы измерения в более старшую (тонна старше килограмма). Смотрим на схему и видим, что стрелка указывающая переход из младших единиц в более старшие, направлена вверх и в конце стрелки указано, что мы должны применить деление:

Теперь нужно узнать сколько килограмм содержатся в одной тонне. В одной тонне содержится 1000 килограмм. А чтобы узнать, сколько тонн составляет 5000 килограмм, нужно 5000 разделить на 1000

5000 : 1000 = 5 т

Значит, при переводе 5000 килограмм в тонны, получается 5 тонн.

Попробуем перевести 6 килограммов в граммы. В данном случае мы переходим из старшей единицы измерения в младшую. Поэтому будем применять умножение.

Сначала надо узнать сколько граммов содержится в одном килограмме. В одном килограмме содержится тысяча граммов:

1 кг = 1000 г

Если в 1 килограмме 1000 граммов, то в шести таких килограммах будет в шесть раз больше граммов. Значит 6 нужно умножить на 1000

6 × 1000 = 6000 г

Значит, при переводе 6 килограммов в граммы, получим 6000 грамм.

история

1790 : Французская академия наук получает заказ от Национального собрания Франции на разработку единой системы мер и весов. Он следует принципам получения основных единиц из натуральных величин, прослеживания всех других единиц до них, умножения и деления их на десятичные дроби. Выбраны следующие основные единицы:

• метр как десятимиллионная часть квадранта земного меридиана ,
• могила (позже: «килограмм») как вес (позже как масса) 1 дм 3 чистой воды максимальной плотности (около 4 ° C).

1832 : Карл Фридрих Гаусс разработал, впоследствии, вместе с Вильгельмом Вебером , систему «абсолютных» электромагнитных единиц, основанных на длине (мм), массе (г) и времени (с) с дробными показателями.

1861 : Основываясь на работе Гаусса и Вебера, Британская ассоциация развития науки (BAAS) определяет электромагнитные единицы с основными единицами m (позже см), g, s. Из-за громоздкости полученных единиц необходимы дополнительные единицы. Введены десятичные кратные основных единиц, в частности вольт как 10 8 и ом как 10 9 электромагнитных единиц cgs . В последующие десятилетия эти подразделения завоевали признание во всем мире. В 1894 году реализация этих единиц была стандартизирована на международном уровне и использовалась для их определения.

1873 : Джеймс Клерк Максвелл предлагает определять единицы длины, времени и массы, используя длину волны, период света и массу молекул.

1875 : Метрическая конвенция подписана 17 государствами. Международное бюро мер и весов является обоснованным.

1889 : На Первой Генеральной конференции по мерам и весам (CGPM) признаются первоначальные измерения метра и килограмма . Вместе со вторым они станут основой нескольких систем агрегатов в последующие годы, особенно МКС и КГС .

1900 : Макс Планк предлагает определять основные единицы, используя физические «константы».

1901 : Джованни Джорджи показывает, что механические и электрические единицы могут быть объединены в согласованную систему с целыми показателями, добавив четвертую базовую величину к системе MBS и переформулировав уравнения электродинамики . Это предложение получило поддержку Международной электротехнической комиссии (МЭК) и Международного союза теоретической и прикладной физики (IUPAP) в 1930-х годах . В 1939 году ответственный комитет BIPM рекомендовал ампер в качестве четвертой базовой единицы.

1948 : Девятая сессия CGPM поручает основу для единой, «практической» системы единиц. Ампер определен в форме, действующей до 2019 года.

1954 : Основываясь на работе CIPM, 10-й CGPM принимает решение о системе с шестью базовыми модулями. Помимо метров, килограммов и секунд (MKS), это ампер, кельвин — до 1968 года называемый «градусами Кельвина» — и кандела .

1960 : На 11-м заседании CGPM этой расширенной системе MKS было присвоено французское название Système International d’Unités (SI) («Международная система единиц»). Измеритель переопределяется по длине волны света.

1971 : На 14-м заседании CGPM крот добавляется как седьмая и последняя базовая единица и помещается на 6-ю позицию между Кельвином и Канделой.

1979 : На 16-й конференции CGPM канделе дано ее текущее определение и она привязана к ватту . Это подключает фотометрические блоки к системе MKS.

1983 : 17-я конференция CGPM переопределяет счетчик, присваивая фиксированное значение скорости света .

2018 : 26-я сессия CGPM решает фундаментальную реформу, вступающую в силу с 20 мая 2019 года: все базовые единицы и, следовательно, все единицы в целом теперь сокращены до семи физических констант, которым присвоены фиксированные значения. Это делает единицы измерения независимыми от реализации и их ограниченную точность.

Система СИ, единицы измерения кратные и дольные

В Международной системе единиц имеется набор приставок к единицам измерения, которые применяют, если численные значения рассматриваемых величин существенно больше или меньше, чем единица системы, которая применяется без приставки. Эти приставки используются с любыми единицами измерения, в системе СИ они являются десятичными.

Приведем примеры таких приставок (табл.3).

Табл.3.

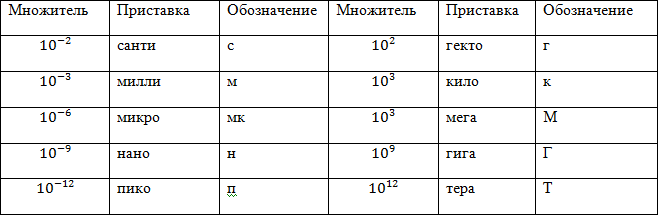
При написании приставку и наименование единицы пишут слитно, так, что приставка и единица измерения образуют единый символ.

Отметим, что единица массы в системе СИ (килограмм) исторически уже имеет приставку. Десятичные кратные и дольные единицы килограмма получают соединением приставки к грамму.