Построение графиков в excel по данным таблицы

Исследование границ ОДЗ и нахождение вертикальных асимптот

На границах функции имеются вертикальные асимптоты, когда односторонние пределы в таких точках бесконечны.

Пример 2

Для примера рассмотрим приграничные точки, равные x=±12.

Тогда необходимо проводить исследование функции для нахождения одностороннего предела. Тогда получаем, что: limx→-12-f(x)=limx→-12-x24x2-1==limx→-12-x2(2x-1)(2x+1)=14(-2)·-=+∞limx→-12+f(x)=limx→-12+x24x-1==limx→-12+x2(2x-1)(2x+1)=14(-2)·(+)=-∞limx→12-f(x)=limx→12-x24x2-1==limx→12-x2(2x-1)(2x+1)=14(-)·2=-∞limx→12-f(x)=limx→12-x24x2-1==limx→12-x2(2x-1)(2x+1)=14(+)·2=+∞

Отсюда видно, что односторонние пределы являются бесконечными, значит прямые x=±12 — вертикальные асимптоты графика.

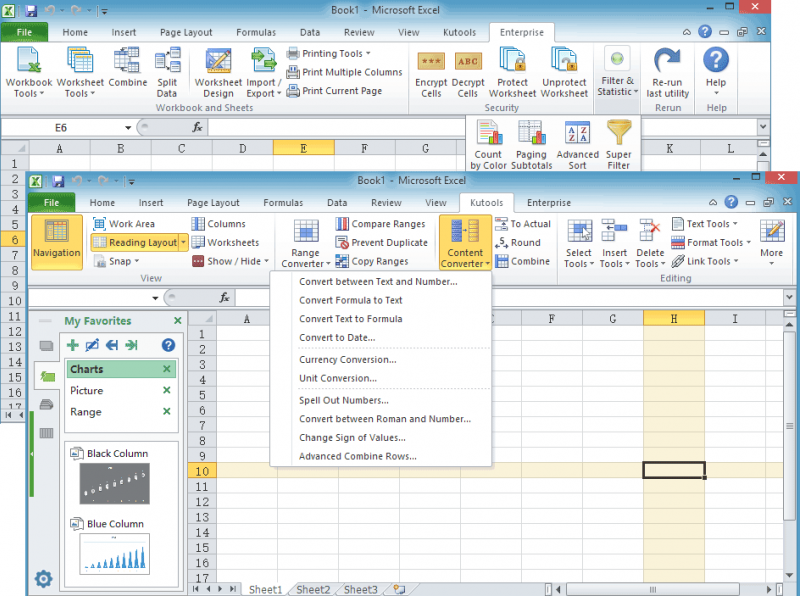
Работа с диаграммами в Экселе

Теперь, когда круговая диаграмма, гистограмма или график готовы, нужно придать им более привлекательный вид, обеспечивающий зрителю наилучшее понимание. К главным параметрам рисунка относятся наименование, легенда и подписи данных; о настройке этих элементов в Экселе будет подробнее рассказано далее.

Выбор названия диаграммы

Задать наименование диаграммы в Excel можно, следуя простому алгоритму:

Выделить щелчком левой клавиши мыши блок с названием.

Ещё раз щёлкнуть, не перемещая указателя, и ввести в текстовом поле новое наименование, более подходящее к случаю.

Другой вариант — щёлкнуть правой клавишей мыши по блоку с наименованием, выбрать в контекстном меню пункт «Изменить текст» и ввести требуемый.

Здесь же, в разделе «Шрифт», юзер может выбрать начертание, кегль и другие параметры текста, подтвердив изменения нажатием на кнопку «ОК».

Чтобы вернуть всё «как было», нужно вновь вызвать контекстное меню и щёлкнуть по строчке «Восстановить стиль».

Настроить название можно, кликнув по полю диаграммы и нажав на «плюсик» в правом верхнем его углу.

В выплывающем меню пользователю нужно выбрать, следует ли размещать название (для отмены достаточно снять галочку в чекбоксе), а также где именно оно должно находиться.

Пункт «Дополнительные параметры» открывает доступ к тонким настройкам названия изображения.

Если название диаграммы было изменено вручную, а теперь требуется вернуть автоматическое наименование (по заголовку соответствующего столбца), следует убрать галочку в чекбоксе или воспользоваться клавишей Delete — рисунок останется без текстового блока.

И снова, нажав на «плюсик», вернуть галочку на место.

Манипуляции с легендой

Ещё большей ясности создатель диаграммы в Экселе может добиться, добавив на рисунок легенду — специальное поле с описанием представленных данных. Сделать это можно следующим образом:

Перейти на вкладку «Конструктор», щёлкнуть по кнопке «Добавить элемент диаграммы» и во вложенном списке «Легенда» выбрать место размещения блока данных: снизу, сверху, справа или слева.

То же самое можно сделать, щёлкнув по полю диаграммы, затем по «плюсику» возле него, установив галочку в чекбоксе с тем же названием и указав в выпадающем меню, где именно будет находиться легенда.

Зайдя в подраздел «Дополнительные параметры», юзер сможет точнее настроить размещение блока, сделать так, чтобы он не накладывался на основной рисунок, задать параметры заливки и текста.

Как можно видеть на примере, подписи в легенде дублируют столбец исходных данных и в таком виде представляют мало интереса.

«Оживить» легенду можно, выделив блок щелчком правой клавиши мыши и зайдя в контекстном меню Excel в подраздел «Выбрать данные».

В новом окне пользователь сможет заменить названия и значения строк и столбцов.

Чтобы придать диаграмме в Экселе приемлемый вид, следует, на время закрыв окно, добавить к таблице ещё один столбец с желаемыми наименованиями рядов данных для блока легенды.

Далее — снова открыв окно, нажать на кнопку «Изменить» в разделе «Подписи горизонтальной оси».

И выбрать, кликнув по обращённой вверх стрелочке в следующем окошке, вновь созданный столбец с названиями, после чего нажать на «ОК».

Ещё раз подтвердив свой выбор в главном окне, юзер закончит изменение подписей легенды.

Теперь блок приобрёл приятный, легко воспринимаемый читателем вид. Убрать блок с поля диаграммы можно, сняв галочку в чекбоксе или воспользовавшись клавишей Delete.

Подписи данных

Легенда позволяет понять соответствие секторов и рядов данных. С нею читать диаграмму, созданную в Excel, становится значительно проще — но ещё лучше будет подписать каждый сектор, разместив на изображении абсолютные или долевые значения, указанные в таблице.

Чтобы добавить на диаграмму, гистограмму или график подписи данных, нужно:

С помощью уже на раз упомянутого «плюсика» вызвать выплывающее меню и установить галочку в чекбоксе «Метки данных».

На рисунке в каждом из секторов появятся абсолютные значения, соответствующие оси ординат.

Автоматически выбранный Экселем вид не слишком эстетичен; имеет смысл сделать подписи более читаемыми, а заодно и выбрать формат представления информации. Для этого следует во вложенном списке «Метки данных» щёлкнуть по любому из предлагаемых системой вариантов.

Перейдя там же в «Дополнительные параметры», юзер сможет определить, какие именно сведения должны содержаться на изображении, отмечая соответствующие чекбоксы.

Так, включённая опция «Линия выноски» позволяет свободно перемещать текстовые поля возле секторов, сохраняя графические связи между ними.

Как строить графики

Для примера возьму такие данные. Есть сотрудники, и количество товара, которое они продали, за определенный месяц. График поможет быстрее понять, какой сотрудник продал больше всего товаров за определенный месяц, или за весь период.

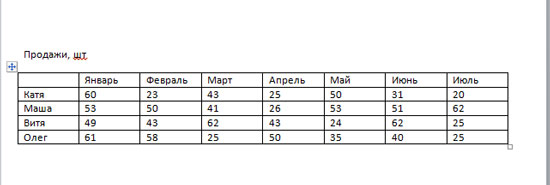
Поставьте курсор в нужном месте документа. Затем перейдите на вкладку «Вставка» и в разделе «Иллюстрации», нажмите на кнопочку с изображением диаграммы.

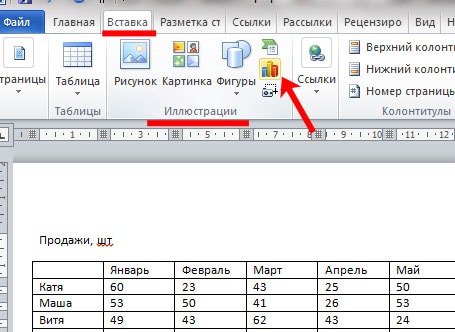
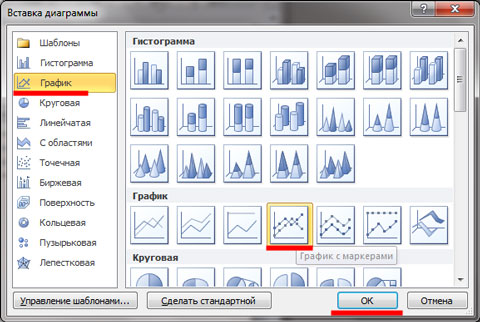
Появится вот такое окно, как на скриншоте ниже. В нем выберите вид диаграммы, который подходит Вам больше всего. Потом нажмите «ОК». Я буду строить с маркерами, но в данном случае можно было бы также сделать гистограмму, или линейчатую диаграмму.

Дальше в Вашем документе появится новая диаграмма, и откроется новый лист Excel с таблицей.

В нее нужно перенести все значения, которые у Вас указаны в таблице в документе Word.

Сначала нужно выбрать правильный диапазон значений в Excel. У меня будет 5 строк (верхняя строка и 4 сотрудника), и 8 столбцов (имена сотрудников и месяцы). Возьмите за правый нижний угол, и выберите нужное Вам количество строк и столбцов.

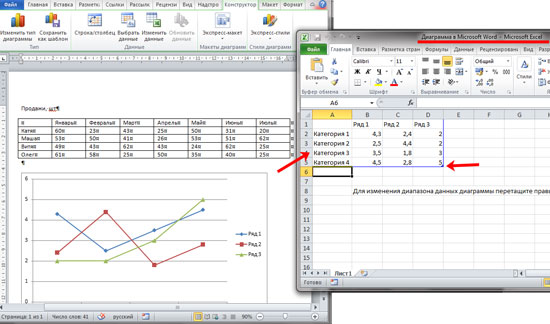
Дальше перенесите все из таблицы в Ворд в Excel.

Когда будете их менять, обратите внимание, что и сам график изменяется

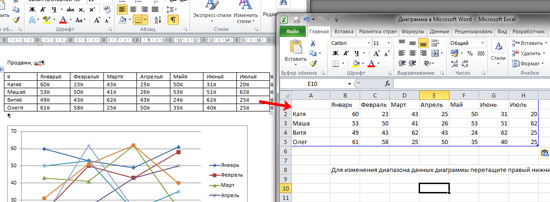
После того, как все в Excel, будет изменено, закройте это окно.

У меня получился вот такой результат.

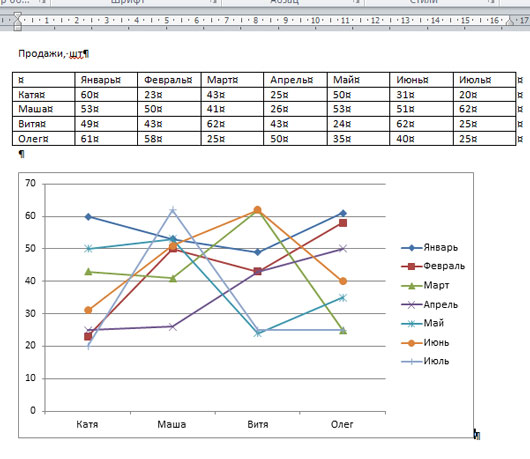
Если кликнуть два раза левой кнопкой мыши по вертикальной (0, 10, 20, 30…), горизонтальной (Катя, Маша…) оси, легенде (Январь, Февраль…) или любому из рядов данных (цветные кривые), откроется окно с настройками.

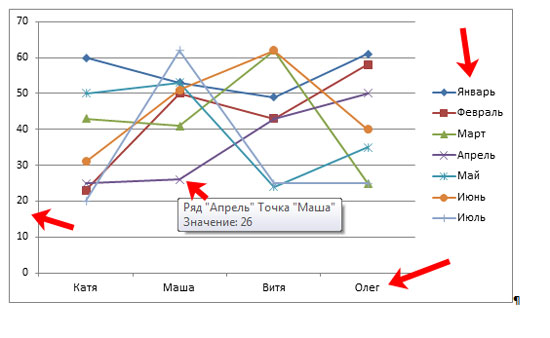
Например, нажмем на кривую со значениями за Апрель, открывается окно «Формат ряда данных». Здесь можно поменять цвет, тип линий и прочее.

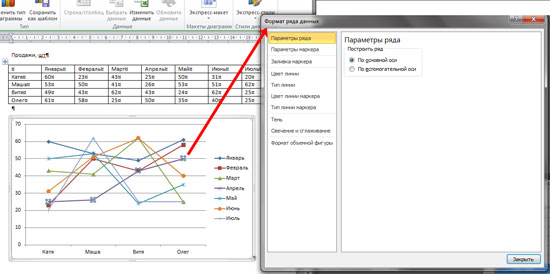
Если кликнуть по горизонтальной оси, откроется окно «Формат оси». В нем можете выбрать необходимые параметры.

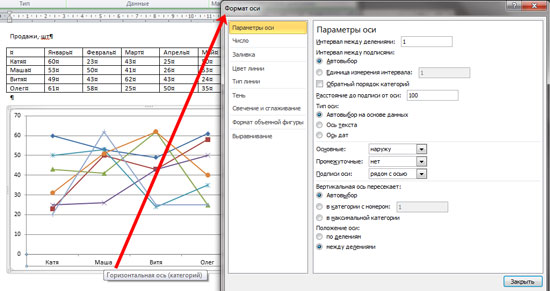
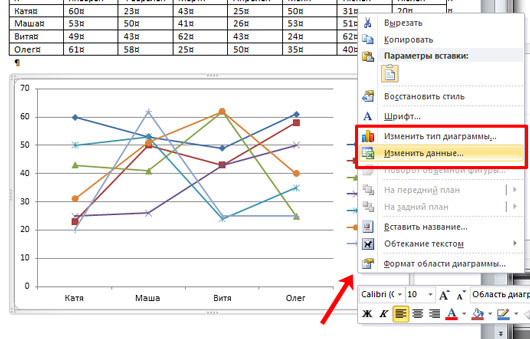
Если кликнуть правой кнопкой мышки по самому графику, откроется контекстное меню. В нем можно «Изменить данные» – появится лист Excel с созданной таблицей, который мы закрыли, «Изменить тип диаграммы» и другое.

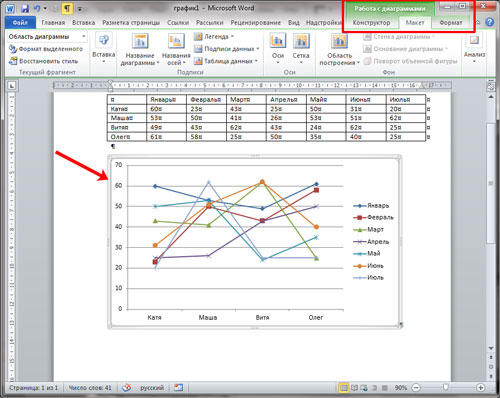
Кликнув по созданному графику, вверху появится вкладка «Работа с диаграммами». В ней Вы увидите еще три дополнительные вкладки: «Конструктор», «Макет» и «Формат». Поклацайте по ним, и посмотрите, как еще можно поменять вид. Например, добавьте название к диаграмме.

После создания, работа с графиком в Ворде ничем не отличается от работы с ним в Excel. Поэтому можете прочесть статью: как сделать график в Excel.

Построение графика по точкам

Чтобы построить график по точкам в декартовой системе координат необходимо задаться исходными данными. Создадим две матрицы-столбца, назовем их X и Y соответственно и заполним их значениями. Для создания матриц-столбцов воспользйтесь панелью Matrix. В панели matrix нажмите на кнопку под названием Matrix and vector. В появившемся окне введите количество строк и столбцов. Для матрицы-столбца количество столбцов будет очевидно ровно одному. Количество строк зависит от количества точек. В нашем случае это 9 точек. После внесения данных нажмите ОК (см. рис. 1)

Рис. 1. Создание матриц-столбцов

В свободном поле mathcad появится пустая матрица-столбец. Поместите курсор в матрицу и с использованием клавиш «стрелка» и «пробел» добейтесь положения курсора, как показано на рисунке 2а ниже. После чего введите с клавитуры символ двоеточия «». У вас должна получиться маска как на рисунке 2b. Теперь вы можете присводить содержимое матрицы какой то переменной. Например переменной X (см. рис. 2c). Заполните матрицу в соответсвии с рисунком 2 и затем повторите те же самые действия для создания матрицы-столбца Y.

Рис. 2. Заполнение матриц-столбцов для графика

На панели Graph найдите кнопку X-Y plot и щелкните по ней левой кнопкой мыши. У вас появится маска для построения графика. В черных прямоугольниках можно вводить имена осей абсцисс и ординат, а так же область отображения кривой графика (см. рис. 3)

Рис. 3. Создание заготовки для графика

Введите под осью абсцисс имя матрицы-столбца X, а слева от оси ординат имя матрицы-столбца Y. В окне графика вы увидите ломаную линию, соединящие координаты, указанные в матрицах столбцах (см. рис. 4)

Рис. 4. График по точкам

Оформление кривой графика по умолчанию, как правило, лишено наглядности и читабельности. Средства mathcad позволяют настраивать отображение графиков. Для этого щелкните 2 раза левой кнопкой мыши по изображению графика и в появившемся окне настройте внешний вид кривой, координатных осей и прочих элементов. Возможности mathcad позволяют: изменять цвет линий, их толщину и тип; нанести сетку на поле графика; подписывать оси координат; изменять формат числовых данных; вводить дополнительную (вторичную, второстепенную) ось ординат. После настройки всех элементов нажмите ОК и вы заметите, что ваш график приобрел более привлекательный вид (см. рис. 5)

Рис. 5. Настройка отображения графика

7 Графики синуса и косинуса

Построим график функции . При этом нам опять пригодятся
часы из разд. 2.1.

Если , то, очевидно, . Когда возрастает от 0 до
, число возрастает от 0 до 1 (представьте себе,
как меняется ордината конца стрелки на наших фирменных часах).
Участок графика для от 0 до изображен на
рис. .
При

Чем ближе к , тем более полого идет наша кривая. Это
происходит потому, что проекция конца стрелки на ось
ординат, колеблясь по отрезку , быстрее всего
движется в середине отрезка и замедляется у его краев: мы
это уже обсуждали в разд. 2.1.

симметричны относительно прямой

Задача 7.1  
Запишите уравнение прямой, касающейся графика функции
в точке с координатами .

Кривая на рис б
центрально симметрична относительно точки
с координатами ; это следует из другой формулы
приведения:
(рис. б).

После того, как у нас есть участок графика функции для

, весь график строится уже просто. В самом деле,
когда конец стрелки прошел путь , стрелка вернулась
в исходное положение; при дальнейшем движении все будет
повторяться. Значит, график будет состоять из таких же кусков,
как на рис б. Окончательно график функции
выглядит так, как на рис. .

Теперь построим график функции . Можно было бы строить его так же, как
мы строили график синуса. Мы, однако, изберем другой путь,
который позволит использовать уже имеющуюся у нас информацию.

Именно, воспользуемся формулой приведения
. Эту формулу можно понимать так: функция
принимает те же значения, что и функция , но на
раньше. Например, функция принимает значение 1 при
, а функция
принимает это же
значение уже при . На графике это означает следующее: для
каждой точки графика есть точка графика ,
у которой ордината та же, а абсцисса на меньше
(рис. ).

сдвинуть график

Итак, мы выяснили, что график косинуса получается преобразованием
(сдвигом) из графика синуса. Случаи, когда график одной функции
можно получить преобразованием из графика другой функции,
интересны и сами по себе, поэтому скажем о них несколько слов.

Как, например, будет выглядеть график функции ? Ясно,
что ординаты точек этого графика получаются из ординат
соответствующих точек графика умножением на 2, так что
наш график изобразится сплошной кривой на рис. . Можно
сказать, что график получается из графика растяжением в два раза вдоль оси
ординат.

сжатием в 2 раза к оси ординат.

Попробуем еще построить график функции 
.
Понятно, что он должен получаться каким-то преобразованием из
графика . На первый взгляд может показаться, что это
преобразование — сдвиг влево на вдоль оси абсцисс, по
аналогии с тем, что изображено на рис. . Однако, если
бы это было так, то вышло бы, например, что функция

принимает значение 1 при

, что не соответствует действительности
(проверьте!). Правильно рассуждать так:
, так что функция
принимает те
же значения, что и функция , но на раньше. Так
что сдвиг влево — не на
, а на (рис. ).

Кривые, являющиеся графиками функций
, где ,
, называются синусоидами. Заметим, что кривой
«косинусоида» вводить не надо: как мы видели, график косинуса
— это та же кривая, что и график
синуса, только иначе
расположенная относительно осей координат.

Задача 7.2  
Каковы координаты точек, помеченных на
рис.  вопросительными знаками?

Задача 7.3  
Возьмите свечу, тонкий лист бумаги и острый нож. Намотайте лист
бумаги на свечу в несколько слоев и аккуратно разрежьте эту свечу
вместе с бумагой наискосок ножом. Теперь разверните бумагу. Вы
увидите, что она оказалась разрезанной по волнистой линии.
Докажите, что эта волнистая линия является синусоидой.

Задача 7.4  
Постройте графики функций:

Замечание. Если вы строите графики
тригонометрических функций на клетчатой бумаге, удобно выбрать
немного разные масштабы по осям, с тем чтобы на оси абсцисс
числу  соответствовало целое число клеточек. Например, часто
выбирают такой масштаб: по оси ординат отрезок длины 1 занимает
две клеточки, по оси абсцисс отрезок длины занимает 6
клеточек.

Задача 7.5  
Постройте графики функций:
а)
;
б)
.

Посмотрим, как выглядят на графиках уже известные нам решения
уравнений и . Эти решения являются
абсциссами точек пересечения горизонтальной прямой
с графиком функций (соответственно ). На
рис. , хорошо видны две серии решений,
получающихся при .

По графикам синуса и косинуса видно, на каких промежутках эти
функции возрастают, а на каких убывают. Ясно, например, что
функция возрастает на отрезках
,

,
,…- одним словом, на
всех отрезках
, где
,
и убывает на всех отрезках
, где

.

Задача 7.6  
На каких отрезках возрастает и на каких убывает
функция ?

Задача 7.7  
Сравните числа:

Задача 7.8  
Расположите в порядке возрастания:
, , , , , .

        Написать комментарий

Как создается график функций

Если Вам нужно вставить его в документ, тогда можете поступить следующим образом. Сначала добавьте график функций в Excel, как это сделать, я рассказывала в отдельной статье, а затем скопируйте его и вставьте в документ Word. После этого, у Вас останется возможность его редактировать в Ворде, как было описано выше: или кликайте по осям, или переходите на вкладку «Работа с диаграммами».

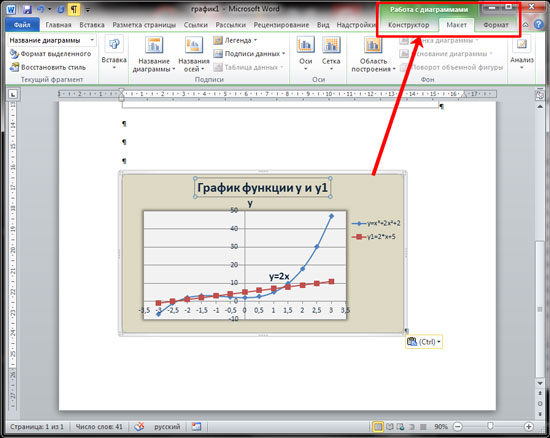
В Интернете также можно найти различные программы, с помощью которых получится сделать график функции в Word. Расскажу про одну из них – «Построитель графиков 1.50».

Это макрос, который нужно установить на компьютер. Затем открываете Ворд и запускаете программу в «Надстройках».

Я скачала файл установки из Интернета. Затем запустила мастер установки.

В установке ничего особого нет. Выберите язык, примите условия лицензионного соглашения, и нажмите «Установить».

Для того чтобы макрос заработал, нужно немного изменить настройки Word. Перейдите на вкладку «Файл» и кликните по пункту «Параметры».

В следующем окне перейдите на вкладку «Центр управления безопасностью» и нажмите на кнопку «Параметры центра управления безопасностью».

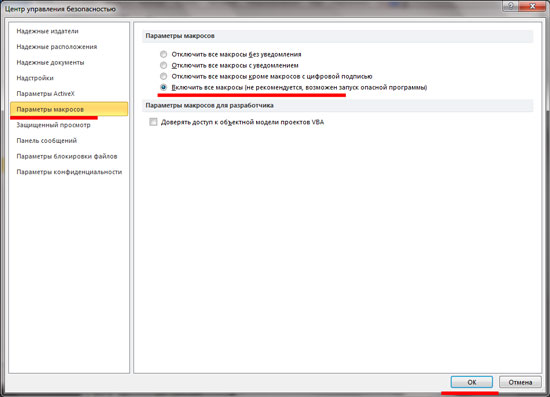
На вкладке «Параметры макросов» поставьте маркер в поле «Включить все макросы». Нажмите «Ок» в этом окне и в предыдущем.

Если Вы не планируете постоянно использовать данный макрос, то, после того, как поработаете с ним, снова зайдите в «Параметры» Word и верните все обратно.

Если на момент установки программы у Вас был открыт документ Word, тогда закройте его и откройте заново.

Затем перейдите на вкладку «Надстройки». Там должна появиться новая иконка, соответствующая макросу. Чтобы запустить макрос, нажмите на нее.

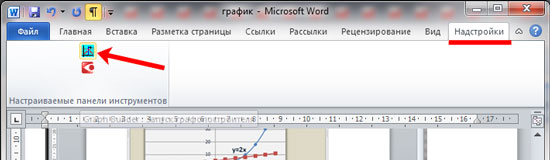
Интерфейс программы на русском языке. Вводите свои значения и рисуйте нужную функцию.

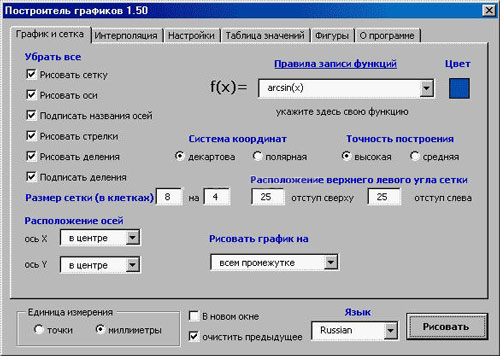
Надеюсь, используя мои рекомендации, у Вас получилось добавить в документ или обычный график, или график функций.

Загрузка…  

Onlinecharts.ru

Онлайн-помощник Onlinecharts.ru строит не графики, а диаграммы практически всех существующих видов. В том числе:

• Линейные.
• Столбчатые.
• Круговые.
• С областями.
• Радиальные.
• XY-графики.
• Пузырьковые.
• Точечные.
• Полярные бульки.
• Пирамиды.
• Спидометры.
• Столбчато-линейные.

Пользоваться ресурсом очень просто. Внешний вид диаграммы (цвет фона, сетки, линий, указателей, форма углов, шрифты, прозрачность, спецэффекты и т. д.) полностью определяется пользователем. Данные для построения можно ввести как вручную, так и импортировать из таблицы CSV-файла, хранимого на компьютере. Готовый результат доступен для скачивания на ПК в виде картинки, PDF-, CSV- или SVG-файлов, а также для сохранения онлайн на фотохостинге ImageShack.Us или в личном кабинете Onlinecharts.ru. Первый вариант могут использовать все, второй — только зарегистрированные.

Построение точечной диаграммы

Как правило, точечная диаграмма используется для построения графиков функций. Например, возьмем функцию y=x^2.

1. Построим таблицу данных из двух столбцов.
    

2. Выделяем данные и вызываем уже упомянутую панель диаграм и выбираем на этот раз точечную.

3. После этого получаем диаграмму, я выбрал с маркерами, на листе.

4. Как уже было ранее показано, перемещаем диаграмму, меняем название, убираем легенду, заливаем фон.

5. Теперь поработаем на вкладке “Конструктор”. Добавим еще пару рядов данных:

6. Переходим на диаграмму и на вкладке “Конструктор” нажимаем кнопку “Выбрать данные”. Появится окно, где мы можем выбрать в качестве диапазона нашу новую таблицу данных.

7. В этом же окне мы можем изменить параметры каждого ряда

   Можно поставить свое произвольное название ряда. Если вдруг Excel неверно взял какой-то ряд в качестве независимой или зависимой переменной, можно произвольно определить нужные диапазоны.

8. Добавляем легенду, меняем название диаграммы и получаем вот такую картинку

Построение обычного графика

Рисовать график в Excel можно только после того, как готова таблица с данными, на основе которой он будет строиться.

1. Находясь на вкладке «Вставка», выделяем табличную область, где расположены расчетные данные, которые мы желаем видеть в графике. Затем на ленте в блоке инструментов «Диаграммы» кликаем по кнопке «График».
2. После этого открывается список, в котором представлено семь видов графиков:
   • Обычный;
   • С накоплением;
   • Нормированный с накоплением;
   • С маркерами;
   • С маркерами и накоплением;
   • Нормированный с маркерами и накоплением;
   • Объемный.

   Выбираем тот, который по вашему мнению больше всего подходит для конкретно поставленных целей его построения.

Дальше Excel выполняет непосредственное построение графика.

Редактирование графика

После построения графика можно выполнить его редактирование для придания объекту более презентабельного вида и облегчения понимания материала, который он отображает.

1. Чтобы подписать график, переходим на вкладку «Макет» мастера работы с диаграммами. Кликаем по кнопке на ленте с наименованием «Название диаграммы». В открывшемся списке указываем, где будет размещаться имя: по центру или над графиком. Второй вариант обычно более уместен, поэтому мы в качестве примера используем «Над диаграммой». В результате появляется название, которое можно заменить или отредактировать на свое усмотрение, просто нажав по нему и введя нужные символы с клавиатуры.

Задать имя осям можно, кликнув по кнопке «Название осей». В выпадающем списке выберите пункт «Название основной горизонтальной оси», а далее переходите в позицию «Название под осью».

Под осью появляется форма для наименования, в которую можно занести любое на свое усмотрение название.

Аналогичным образом подписываем вертикальную ось. Жмем по кнопке «Название осей», но в появившемся меню выбираем «Название основной вертикальной оси». Откроется перечень из трех вариантов расположения подписи: повернутое, вертикальное, горизонтальное. Лучше всего использовать повернутое имя, так как в этом случае экономится место на листе.

На листе около соответствующей оси появляется поле, в которое можно ввести наиболее подходящее по контексту расположенных данных название.

Если вы считаете, что для понимания графика легенда не нужна и она только занимает место, то можно удалить ее. Щелкните по кнопке «Легенда», расположенной на ленте, а затем по варианту «Нет». Тут же можно выбрать любую позицию легенды, если надо ее не удалить, а только сменить расположение.

Построение графика в полярных координатах в mathcad

Введите функцию, которую необходимо построить в полярных координатах. Для примера возьмем y(x):=2*sin(3*x+0.5)

Для построения графика в полярных координатах нажмите кнопку Polar Plot из панели Graph

Рис. 13. Создание загатовки для графика в полярных координатах

Вы увидете пустое поле графика. В черном маркере слева введите имя введенной функции y(x). В маркере снизу введите аргумент x и нажмите enter. Вы увидете «трилистник». Внешний вид графика можно настроить щелкнув два раза по графику левой кнопкой мыши. В появившемся окне представлен широкий набор инструментов для настройки отображения.

Схема исследования поведения функций, применяемая для построения графиков функций

      Для построения   y = f (x)   желательно сначала провести исследование поведения функции   y = f (x)   по следующей схеме.

1. Найти   D ( f ).

2. Выяснить, является ли функция   y = f (x)   или

3. Выяснить, является ли функция   y = f (x)  

4. Найти асимптоты графика функции.

5. Вычислить производную функции   f ‘ (x) .

6. Найти функции   y = f (x) .

7. Найти интервалы и функции   y = f (x) .

8. Найти   y = f (x) .

9. Найти точки пересечения   y = f (x)   с .

   Если не удается точно найти нули функции, то есть точки, в которых график функции пересекает ось абсцисс   Ox,   то нужно попытаться найти интервалы, на которых нули функции располагаются. Часто эти интервалы удается найти, зная точки максимума и минимума функции.

10. Вычислить функции   f »  (x) .

11. Найти интервалы, на которых функция   y = f (x)   , а также интервалы, на которых функция   y = f (x)  .

12. Найти графика функции  y = f (x) .

      Замечание. Желательно рисовать схему поведения функции параллельно с проведением исследования свойств функции по описанному выше плану.

Графики обратных тригонометрических функций

Построим график арксинуса

Перечислим основные свойства функции :

Область определения: , не существует значений вроде  или

Область значений: , то есть,  функция  ограничена.

Арксинус – функция нечетная, здесь минус опять же выносится: .

В практических вычислениях полезно помнить следующие значения арксинуса: , , . Другие распространенные значения арксинуса (а также других «арков») можно найти с помощью таблицы значений обратных тригонометрических функций.

Построим график арккосинуса

Очень похоже на арксинус, свойства функции сформулируйте самостоятельно. Остановлюсь на единственном моменте. В данной статье очень много разговоров шло о четности  и нечетности функций, и, возможно, у некоторых сложилось впечатление, что функция обязательно должна быть четной или нечетной. В общем случае, это, конечно, не так. Чаще всего, функция, которая вам встретится на практике – «никакая». В частности, арккосинус не является четной или нечетной функцией, он как раз «никакой».

Построим график арктангенса

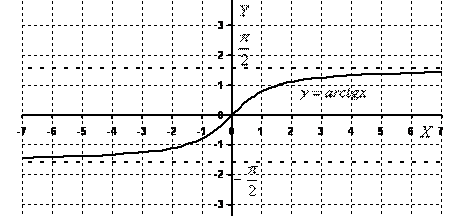
Всего лишь перевернутая ветка тангенса.
Перечислим основные свойства функции :

Область определения:

Область значений: , то есть,  функция  ограничена.
У рассматриваемой функции есть две асимптоты: , .

Арктангенс – функция нечетная: .

Самые «популярные» значения арктангенса, которые встречаются на практике, следующие: , .

К графику арккотангенса  приходится обращаться значительно реже, но, тем не менее, вот его чертеж:

Свойства арккотангенса вы вполне сможете сформулировать самостоятельно. Отмечу,  что арккотангенс, как и арккосинус, не является четной или нечетной функцией.

Пожалуй, для начала хватит. К этой странице придется частенько обращаться в ходе изучения самых различных разделов курса высшей математики.

Ну что, смертнички, полетаем? =)

Тогда надеваем парашюты и готовимся к преобразованиям графиков.

Желаю успехов!

(Переход на главную страницу)

Построение графика линейной функции в Excel

Построение графиков в Excel 2016 значительно улучшилось и стало еще проще чем в предыдущих версиях. Разберем пример построения графика линейной функции y=kx+b на небольшом интервале .

Подготовка расчетной таблицы

В таблицу заносим имена постоянных  k и b в нашей функции. Это необходимо для быстрого изменения графика без переделки расчетных формул.

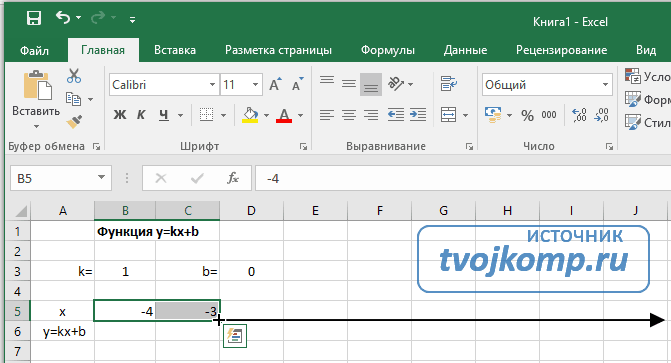
Установка шага значений аргумента функции

Далее строим таблицу значений линейной функции:

• В ячейки A5 и A6 вводим соответственно обозначения аргумента и саму функцию. Запись в виде формулы будет использована в качестве названия диаграммы.
• Вводим в ячейки B5 и С5 два значения аргумента функции с заданным шагом (в нашем примере шаг равен единице).
• Выделяем эти ячейки.
• Наводим указатель мыши на нижний правый угол выделения. При появлении крестика (смотри рисунок выше), зажимаем левую кнопку мыши и протягиваем вправо до столбца J.

Ячейки автоматически будут заполнены числами, значения которых различаются заданным шагом.

Автозаполнение значений аргумента функции

Далее в строку значений функции в ячейку B6 записываем формулу =$B3*B5+$D3

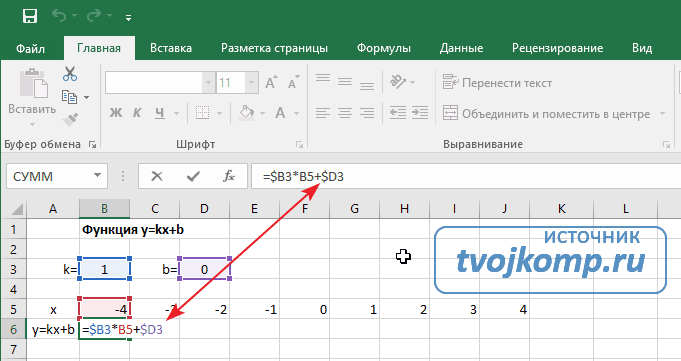
Запись расчётной формулы для значений функции

Чтобы завершить ввод формулы нажмите клавишу Enter или галочку слева от строки формул вверху над таблицей.

Копируем эту формулу для всех значений аргумента. Протягиваем вправо рамку от ячейки с формулой до столбца с конечными значениями аргумента функции.

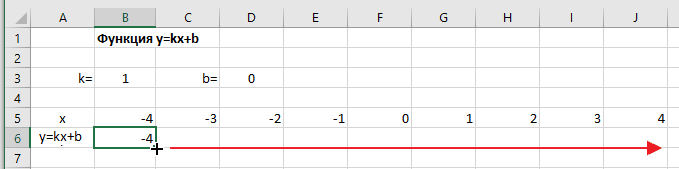
Копирование формулы

Построение графика функции

Выделяем прямоугольный диапазон ячеек A5:J6.

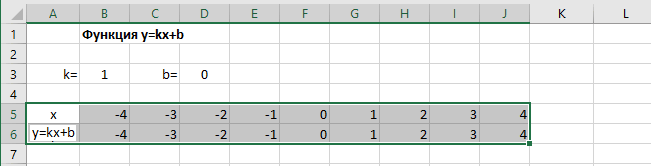
Выделение таблицы функции

Переходим на вкладку Вставка в ленте инструментов. В разделе Диаграмма выбираем Точечная с гладкими кривыми (см. рисунок ниже).Получим диаграмму.

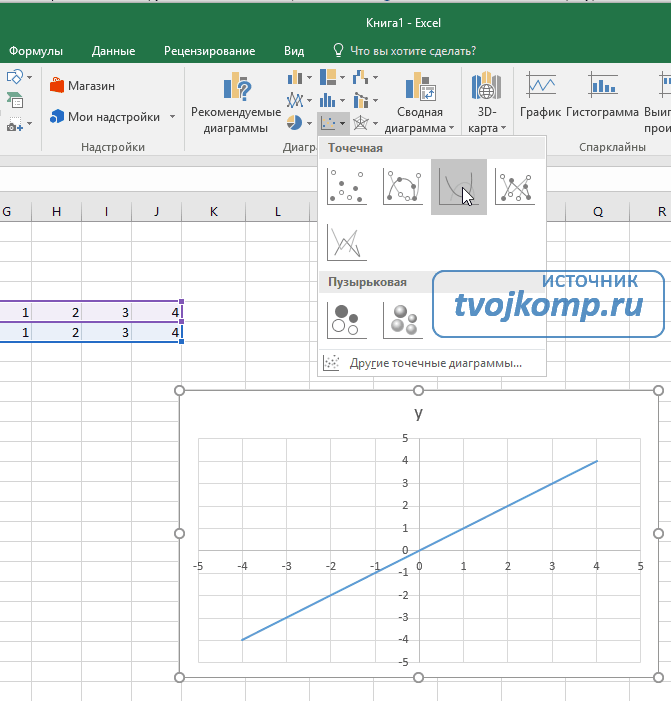
Построение диаграммы типа «График»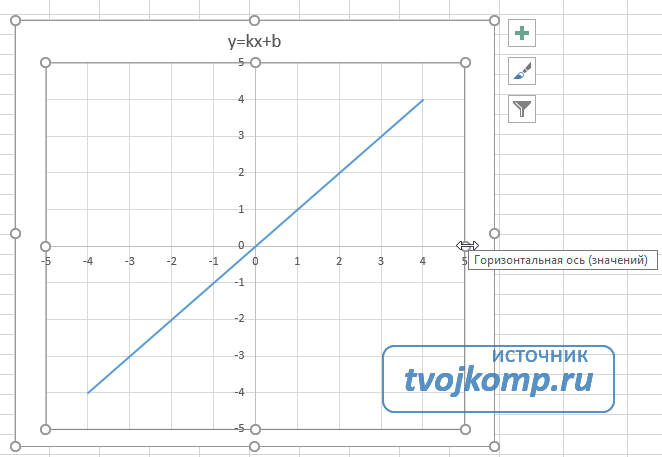
График линейной функции

Теперь можно ввести новые значения постоянных k и b для изменения графика. И видим, что при попытке изменить коэффициент график остается неизменным, а меняются значения на оси. Исправляем. Кликните на диаграмме, чтобы ее активировать. Далее на ленте инструментов во вкладке Работа с диаграммами на вкладке Конструктор выбираем Добавить элемент диаграммы — Оси — Дополнительные параметры оси..

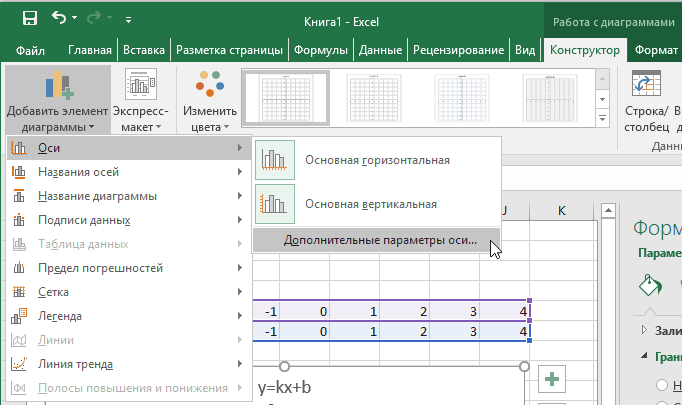
Вход в режим изменения параметров координатных осей

В правой части окна появиться боковая панель настроек Формат оси.

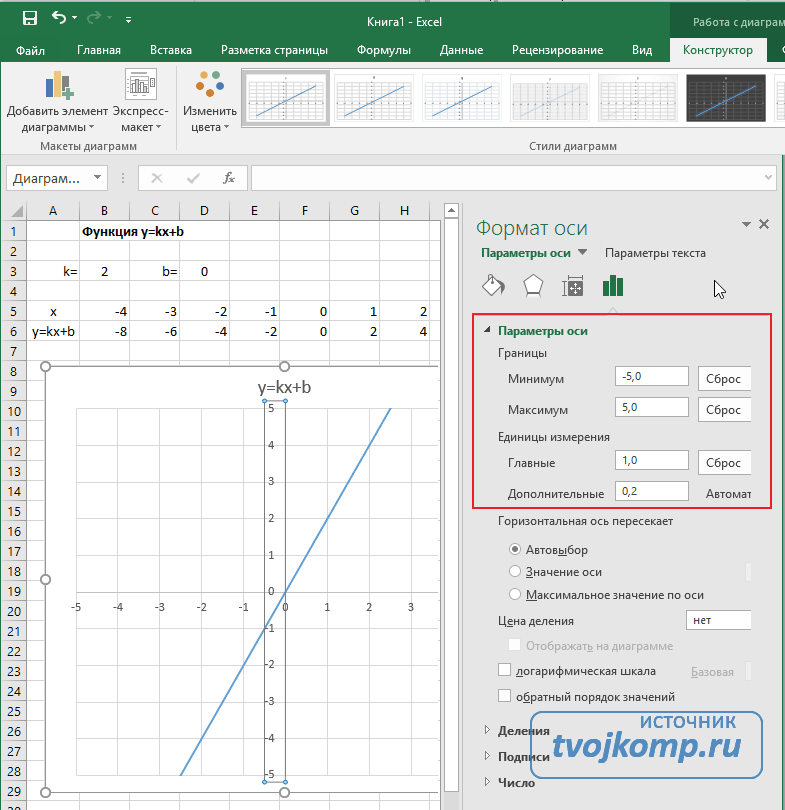
Редактирование параметров координатной оси

• Кликните на раскрывающийся список Параметры оси.
• Выберите Вертикальная ось (значений).
• Кликните зеленый значок диаграммы.
• Задайте интервал значений оси и единицы измерения (обведено красной рамкой). Ставим единицы измерения Максимум и минимум (Желательно симметричные) и одинаковые для вертикальной и горизонтальной осей. Таким образом, мы делаем мельче единичный отрезок и соответственно наблюдаем больший диапазон графика на диаграмме.И главную единицу измерения — значение 1.
• Повторите тоже для горизонтальной оси.

Теперь, если поменять значения K и b , то получим новый график с фиксированной сеткой координат.

Как построить график онлайн?

Даже если преподаватель требует вас сдавать задание, написанное от руки, с чертежом на листке в клеточку, вам будет крайне полезно во время решения построить график в специальной программе (или сервисе), чтобы проверить ход решения, сравнить его вид с тем, что получается вручную, возможно, найти ошибки в своих расчетах (когда графики явно ведут себя непохоже).

Ниже вы найдете несколько ссылок на сайты, которые позволяют построить удобно, быстро, красиво и, конечно, бесплатно графики практически любых функций. На самом деле таких сервисов гораздо больше, но стоит ли искать, если выбраны лучшие?

Графический калькулятор Desmos

Desmos.com
Невероятно гибкий и функциональный графический калькулятор. Интутивно понятно вводятся формулы (прямо на ходу преобразуются), автоматически подбираются масштаб и цвета графика для максимальной наглядности. Например, для функции $y(x)=\frac{x^3}{4(x-2)^2}$ буквально за минуту построены основной график и асимптоты, вот что получилось:

При этом сайт сам пометил важные точки на графике (см. серым): локальный экстремум, пересечение с осями.

Вы можете менять масштаб, цвета, вид линий; добавлять на график точки, линии, кривые, табличные данные и даже анимацию!

Посмотрите, какую красоту Desmos умеет рисовать (точнее, его пользователи):

Сайт для построения графиков y(x).ru

y(x).ru
Это уже наш продукт, возможно, не такой красивый и интерактивный, но вполне подходящий для учебных целей. Можно строить онлайн несколько графиков одновременно, при этом выбирать и обычный, и параметрический вид, и даже задание в полярных координатах. Цвет и масштаб можно менять вручную. Вот так вводятся графики:

И такой график получается в итоге:

Из минусов можно заметить, что вводить, например, горизонтальные асимптоты не так просто: если в Desmos мы просто написали $x=2$, то здесь пришлось вводить параметрическую функцию $x(t)=2, y(t)=t$. Цвета и масштаб тоже пришлось подбирать вручную (иначе все графики оказались бы красными и мелкими).

Другие сайты

Еще несколько сервисов, которые обладают меньшим удобством/функциональностью, но тоже достойны внимания:

• ru.numberempire.com Можно построить сразу несколько функций, цвета подбираются автоматически, график интерактивный (положение и масштаб меняются мышкой).
• mathsolution.ru Можно строить несколько графиков, выбирая толщину линий и цвет, скрывать/отображать сетку, менять масштаб, сохранять картинки в файл.
• easyto.me При построении нескольких графиков на одном поле предыдущие не редактируются. В остальном функции как у прежних: выбор цвета, толщины линии, масштаба чертежа.
• grafikus.ru Кроме обычных графиков можно также строить трехмерные (3d). Можно построить несколько графиков разного типа (обычный,параметрический, в полярных координатах). Цвет и толщину линии выбрать нельзя. Интерактивности нет