Сложный процент

Наращение

Наращение – это процесс приведения текущей стоимости денег к будущей. Наращение позволяет получить оценку той суммы, на которую можно рассчитывать в будущем, инвестировав некоторым образом исходную сумму. Это процесс, обратный дисконтированию.

Базовая формула наращения, если ставка доходности одинакова для каждого периода:

Экономический смысл наращения

Сейчас у нас есть 1 000 000 рублей. Мы хотим на 3 года его инвестировать на биржу, ожидаемая доходность инвестиций 15%. Какая сумма будет на счете через 3 года?

Наращение делают по сложному проценту. Возможно делать наращение по разным ставкам (в каждый период своя доходность).

По сути наращение и есть работа сложных процентов на будущие периоды.

Понимание силы сложных процентов позволяет более рассудительно и долгосрочно относиться к инвестициям.

5954 Всего просмотров 1 Сегодня просмотров

Сравнение эффектов от простого и сложного процента

Базовые показатели для примеров одинаковые:

• размер первоначального вклада равен 95 000 руб.;
• срок депозита зафиксирован на отметке 7 лет;
• годовую величину процентной ставки стороны согласовали на уровне 11%;
• выплата процентов – по итогам каждого года.

В первом случае будет использоваться простой процент определения дохода по вкладу, а во втором вкладчик воспользуется правом на капитализацию процентов. В обеих ситуациях не будут производиться дополнительные взносы на протяжении срока действия договора по вкладу. Итоги расчетов за каждый год представлены в таблице:

Период	Простой процент	Сложный процент
Базовая сумма, руб.	Начисленный доход за год, руб.	Базовая сумма, руб.	Доход за год, руб.
1 год	95 000,00	10 450,00	95 000,00	10 450,00
2 год	10 450,00	105 450,00	11 599,50
3 год	10 450,00	117 049,50	12 875,45
4 год	10 450,00	129 924,95	14 291,74
5 год	10 450,00	144 216,69	15 863,84
6 год	10 450,00	160 080,53	17 608,86
7 год	10 450,00	177 689,39	19 545,83
Итого:	х	73 150,00	х	102 235,22

На примере видно, что общая прибыль за 7 лет при капитализации процентов будет значительно выше, чем на условиях перевода дохода на счет вкладчику. По итогам семи лет разница составит 29 085,22 руб. (102 235,22 – 73 150). Динамика увеличения разрыва между уровнем доходности по простому и сложному проценту хорошо прослеживается на сравнительном графике. При одинаковых исходных данных с каждым годом прибыль за счет капитализации увеличивается более быстрыми темпами, а при отсутствии капитализации доход накапливается с одинаковой скоростью.

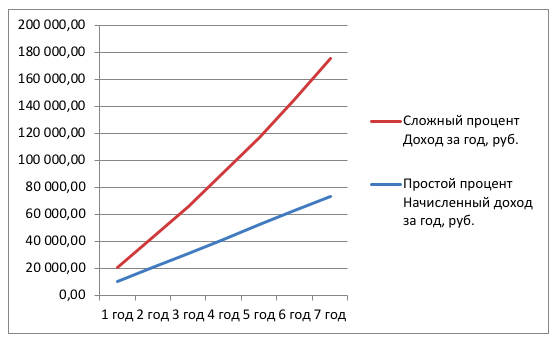
В случае с простыми процентами у вкладчика есть возможность регулярно получать доход с депозита и тратить его. При капитализации процентов этого шанса не будет – производимые начисления не будут выплачиваться владельцу средств до момента окончания срока действия договора по вкладу. Если имеется необходимость просто сохранить деньги и получить регулярный доход (как прибавку к зарплате или в качестве основного источника заработка), то предпочтение стоит отдавать простым депозитам. Но если целью является эффективное приумножение капитала, лучшим вариантом станет инвестирование с капитализацией доходов.

Среднегодовая доходность

Для сравнения разных способов инвестиций на дистанции нам необходимо уметь считать среднегодовую доходность наших инвестиций. Формула при условии, что мы один раз инвестировали деньги и потом получили некий результат:

Пример: в 2014 году мы инвестировали на биржу 100 000 рублей. Через 3 года у нас на счету стало 285 000 рублей. Рассчитаем среднегодовую доходность за три года:

Самопроверка:

Экономический смысл: если бы выбирали между банком и биржей по доходности, то нам нужно было бы найти банк, который предлагает ставку в размере 41,78% или выше на протяжении 3 лет ежегодно.

Формула для расчета среднегодовой доходности, если нам известны результаты инвестиций по годам:

Пример: в первый год инвестор заработал 15%, во второй потерял -10% и в третий заработал 29%. Какова его среднегодовая доходность?

Несмотря на два очень удачных года среднегодовая доходность инвестора оказалась на уровне всего лишь 10,11%.

Периоды падения очень отрицательно сказываются на среднегодовой доходности!

Давайте ещё раз сделаем самопроверку и окончательно поймем экономический смысл. Посчитаем сначала с учетом ежегодной доходности по каждому году результат инвестирования:

Разница в 15 рублей получилась за счет округления 10,11%.

Плавная доходность лучше всплесков

Многие инвесторы (особенно новички) гонятся за огромными доходностями, получают их в один год и терпят “незначительные” убытки в следующий год. Давайте рассмотрим ещё один показательный случай из практики, что “медленные инвесторы” в итоге выигрывают:

Инвестор 1 получил доходность в первый год +90%, во второй год убыток в размере -21% и в третий год доходность в размере +15%.

Инвестор 2 получил доходность в первый год +21%, во второй год +32% и в третий год всего лишь +9%.

Кто заработал больше?

1.9*0.79*1.15 = 1.72615

Среднегодовая доходность первого 19,96%.

1.21*1.32*1.09 = 1.784112

Среднегодовая доходность второго 21,29%.

“Сверхдоходность” в 90% не спасла “быстрого” инвестора. Его итоговый результат оказался ниже, чем результат работы “плавного” инвестора.

Минусы вредны для портфеля. Если портфель упал на 20%, то ему надо заработать 25%, чтобы хотя бы восстановиться. 

Сколько нужно зарабатывать после падений для восстановления первоначальной суммы на счете

Что из себя представляют сложные проценты?

Сложные проценты – это проценты по депозиту или займу, учитывающие как вашу первоначальную сумму, так и проценты, накопленные этой суммой за предыдущие периоды. Поскольку вы зарабатываете проценты не только на основную сумму каждый период, но и на накопленную сумму, вы получаете больше прибыли от вложенных средств.

Со сложными процентами вы добавляете заработанные проценты обратно на свой основной баланс, и затем это приносит вам еще больше процентов, тем самым увеличивая вашу прибыль.

Допустим, у вас есть 1000 долларов на сберегательном счете, на который вы получаете 5% годовых. В первый год вы заработаете 50 долларов, в итоге ваш баланс составит 1050 долларов. Во второй год вы заработаете 5% на балансе в 1050 долларов, что составляет 52,50 доллара, что даст вам новый баланс в размере 1102,50 долларов в конце второго года.

Благодаря магии сложных процентов рост баланса вашего сберегательного счета со временем будет ускоряться, поскольку вы зарабатываете проценты на все более крупных остатках. Если вы оставите 1000 долларов на сберегательном счете на 30 лет, продолжая получать 5% годовых и никогда не добавляете ни копейки на счет, в итоге вы получите остаток в размере 4321,94 доллара.

Проценты могут быть увеличены или добавлены обратно в основную сумму в разные промежутки времени. Например, проценты могут начисляться ежегодно, ежемесячно, ежедневно или даже постоянно. Чем чаще начисляются проценты, тем быстрее растет баланс вашего счета.

Если вы начали с остатком на сберегательном счете в 1000 долларов, но заработанные вами проценты увеличивались ежедневно, а не ежегодно, через 30 лет вы получите общий баланс в размере 4481,23 доллара. Вы заработали бы дополнительно 160 долларов за счет более частого начисления процентов.

Пример расчета с реальным банковским вкладом

Выше мы рассмотрели упрощенные примеры работы сложного процента. На самом деле банки используют немного усложненную формулу.

Ставка процентов представляется как

Формула универсальная и позволяет сделать вычисление для разных типов депозитов. Таким образом, наша основная формула стала чуть-чуть сложнее:

Математическое понятие «геометрическая прогрессия» помогает работать банковскому вкладу с капитализацией гораздо более эффективно, чем без капитализации. Человеческий мозг не всегда может представить разницу или она поначалу ему кажется не существенной. В действительности, на значительных отрезках времени сложный процент начинает играть огромную роль при построении капитала.

Эффективная процентная ставка по вкладу

Эта характеристика актуальна только для вкладов с капитализацией процентов. В связи с тем, что проценты не выплачиваются а идут на увеличение суммы вклада, очевидно, что если ежемесячно возрастает сумма вклада, то и вновь начисленные на эту сумму проценты также будут выше, как и конечный доход.

Если рассчитать, сколько процентов было начислено к начальной сумме к концу срока вклада, эта величина и будет являться эффективной процентной ставкой.

Формула расчета эффективной ставки:

где
N — количество выплат процентов в течение срока вклада,T —  срок размещения вклада в месяцах.

Эта формула не универсальна. Она подходит только для вкладов с капитализацией 1 раз в месяц, период которых содержит целое количество месяцев. Для других вкладов (например вклад на 100 дней) эта формула работать не будет.

Однако есть и универсальная формула для рассчета эффективной ставки. Минус этой формулы в том, что получить результат можно только после рассчета процентов по вкладу.

Эта формула подходит для всех вкладов, с любыми сроками и любой периодичностью капитализации. Она просто считает отношение полученного дохода к начальной сумме вклада, приводя эту величину к годовым процентам. Лишь небольшая погрешность может присутствовать здесь, если период вклада или его часть выпала на високосный год.

Именно этот метод используется для рассчета эффективной ставки в представленном здесь депозитном калькуляторе.

Как было до 2021 года

Налог начислялся в случаях, если ставка по вкладу превышала ключевую на 5 и более процентов. Размер налога был 35% и 30% для резидентов и нерезидентов соответственно. Начислялся он не на весь доход во вкладу, а только на разницу между доходом, вычисленным по пороговой ставке (ключевая ставка + 5%) и реально полученным доходом.

Как стало с 2021 года

• Налоговая ставка теперь 13% для всех.
• Введена необлагаемая сумма дохода. Все, что выше — облагается налогом. Количество вкладов не имеет значения, считается общая сумма на всех вкладах.
• Необлагаемый доход рассчитывается следующим образом:

• Налог платится 1 раз в год за все вклады.
• ФНС рассчитывает сумму налога самостоятельно и направляет уведомление.
• Срок уплаты — 1 декабря года, следующего за расчетным.

В качестве примера возьмем 2021 год.

1. У Васи есть 2 вклада в разных банках. В первом банке 500 000 руб. под 5%, во втором банке 800 000 руб под 4%.
2. Ключевая ставка ЦБ на 1 января 2021 года была 4.25%.
3. Сумма необлагаемого дохода едина для всех вкладов и составляет 1 000 000 × 4.25% = 42 500 руб. С этой суммы налог платить не нужно.
4. Доход по вкладам васи за год составит: в первом банке — 25 000 руб., во втором — 32 000 руб. Всего — 57 000 руб.
5. Разница между фактическим и необлагаемым доходом составит 57 000 — 42 500 = 14 500 руб. Это тот доход, с которого необходимо заплатить НДФЛ.
6. Размер НДФЛ = 14 500 × 13% = 1 885 руб.

Как это работает в реальной жизни: примеры из истории

Бенджамин Франклин, умерший в 1790 году, завещал городам Бостону и Филадельфии по 2000 долларов, с обязательством не тратить эти средства в течение 200 лет и держать их на банковском депозите. Мэрии городов направляли деньги на выдачу займов, не расходуя полученную прибыль (фактически, реинвестируя их в новые займы). В результате через 200 лет у городов было 5 млн. и 2 млн. долларов соответственно.

Другой пример из американской истории. В 17-м веке голландцы выкупили у туземных индейцев территорию Манхеттена за 1000 долларов (по сегодняшним ценам). Если бы индейцы внесли эти деньги на депозит под 10%, то сегодня они бы обладали суммой в 100 трл.долларов.

Что такое сложные проценты

Те, кто хоть раз размещал капитал, независимо от выбранного инструмента (депозит, облигации или акции), наверняка, слышал о сложных процентах. Исходя из названия понятно, что это именно доходность капитала. Но почему же она является сложной и как ее считать?

Если говорить простыми словами, проценты, полученные от капитала, инвестор не расходует на собственные нужды, а вкладывает их в тот же инструмент. В результате этого на следующую дату выплаты дохода они будут начисляться не только на сумму основного капитала, но и на проценты, вложенные в прошлом периоде. Этот маневр также называется реинвестированием, а в банковской среде он более известен как капитализация процентов.

Подобная политика реинвестирования процентов позволяет с каждым годом увеличивать не только сумму основного капитала, но и значительно повысить его доходность. При этом, чем больше срок вложения, тем сильнее заметен положительный эффект, если сравнивать его с расчетом простых процентов. Так, даже относительно небольшую сумму вложений можно увеличить в разы уже через 4-5 лет, а спустя более долгий период времени можно сколотить неплохой капитал. Конечно, многое зависит и от выбранного инструмента. Но, тем не менее, сложные проценты всегда дают положительный эффект.

Преимущества инвестирования с применением сложных процентов:

• Накопительный эффект. При инвестировании с капитализацией на конец периода инвестор будет иметь только первоначальную сумму основного капитала и начисленные за последний период проценты. Используя политику сложных процентов, инвестор на конец периода будет иметь первоначальную сумму со всеми начисленными за весь период процентами.
• Ежегодное повышение суммы доходности, даже если основная ставка инструмента не меняется. За счет увеличения суммы основного капитала на начисленные в прошлом периоде проценты, увеличивается и сумма для исчисления доходности в текущем промежутке времени.
• Возможность увеличения первоначального капитала без дополнительных вложений.

Основные определения

Когда мы сравниваем разные части целого, мы используем такие понятия, как половина (1/2), треть (1/3), четверть (1/4). Это удобно: отрезать половину пирога, пройти треть пути, закончить первую четверть в школе.

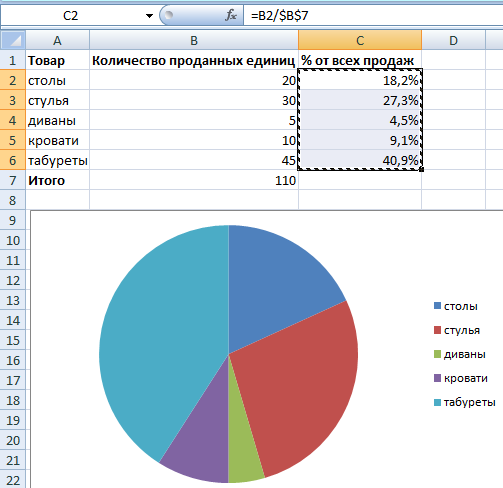
Чтобы сравнивать сотые доли, придумали процент (1/100): с латинского языка — «за сто».

Процент — это одна сотая часть от любого числа. Обозначается вот так: %.

Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить число на 100, как в примере выше.

А если нужно перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Например:

0,18 = 0,18 · 100% = 18%.

А вот, как перевести проценты в десятичную дробь — обратным действием:

18 : 100 = 0,18.

Выразить дробь в процентах просто. Для перевода сначала превратим её в десятичную дробь, а потом используем предыдущее правило:

В детской школе Skysmart ученикам помогает считать проценты веселый енот Макс. Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем. А еще развивающие игры, квесты и головоломки на любой возраст и уровень.

Ключевые различия между простым интересом и сложным интересом

Ниже приведены основные различия между простым и сложным интересом:

1. Проценты, начисляемые на основную сумму за весь срок кредита, известны как простые проценты. Проценты, начисляемые как на основную сумму, так и на ранее заработанные проценты, называются сложными процентами.
2. Сложный процент дает высокую доходность по сравнению с простым процентом.
3. В Простом Проценте основное значение остается постоянным, в то время как в случае Сложного Процента Основное значение изменяется из-за эффекта сложения.
4. Темпы роста Простых процентов ниже, чем сложных процентов.
5. Расчет простого процента прост, а расчет сложного процента сложен.

пример

Предположим, Алекс депонировал рупий. 1000 в банк под 5% годовых (простой и составной) в год на 3 года. Узнайте общий интерес, который он получит в конце третьего года?

Решение : здесь P = 1000, r = 5% и t = 3 года

Простой интерес =

Сложный процент =

Заключение

Проценты — это плата за использование чужих денег. Существует много причин для выплаты процентов, таких как временная стоимость денег, инфляция, альтернативные издержки и фактор риска. Простой процент быстро рассчитывается, но сложный процент практически сложен. Если вы рассчитываете как простой процент, так и сложный процент для данного принципала, ставки и времени, вы всегда обнаружите, что сложный процент всегда выше, чем простой процент из-за сложного эффекта на него.

Понятие простых процентов и как они рассчитываются

Простые проценты – это проценты, начисляющиеся лишь на первоначальную величину вклада, независимо от количества периодов и их продолжительности. Они считаются один раз по окончанию срока депозита. Это обозначает, что сумма процентов за предыдущий период не учитывается при расчете в следующем. 

Метод расчета простых процентов основан на принципе наращения денег по арифметической прогрессии. Допустим, инвестор в начале года положил в банк депозит на сумму 100 000 руб. под 10% годовых:

• через год он получит сумму, равную первоначально внесенным деньгам плюс начисленные проценты: 100 000 + 10 000 (чтобы высчитать процент нужно сумму вклада умножить на ставку и разделить на 100) = 110 000 (руб.);
• через 2 года сумма составит: 100 000 + (10 000 х 2) = 120 000 (руб.);
• через N лет вкладчик получит: 100 000 + (10 000 х N).

Поскольку банки указывают ставку за год, то чтобы определить доход за другой период (к примеру, 3 месяца), применяя простую ставку процентов, формула будет такой:

S = (P x I x Т / K) / 100, где:

S– сумма насчитанных процентов (руб.);

P– начальная сумма вложенных средств;

I– процентная ставка за год;

Т – срок действия вклада в днях;

K– число дней в году.

То есть при вкладе 100 000 руб. на 3 месяца под 10% годовыхвычисление простых процентовбудет выполняться так:

(100 000 х 10 х 92 / 365) / 100 = 2520,55 (руб.).

Получается, что в конце срока вкладчик получит на руки внесенные 100 000 руб. плюс 2520,55 руб. дохода, т.е. 102 520,55 руб.

Это интересно: Обязанности таможенного брокера, кто это такой

Простой и сложный, в чем отличие

В математике один процент – одна сотая часть числа. Говоря о банковском проценте, обычно подразумевают сумму денег, начисленную по определенным правилам и скопившуюся к конкретному сроку.

Все условия начисления процентов обязательно указываются в договоре между сторонами. Имеют значение такие факторы:

• размер годовой процентной ставки,
• капитализация процентов,
• срок договора,
• порядок выплаты процентов.

Кроме размера ставки, т.е количества начисленных за год процентов, на конечную сумму существенно влияет наличие или отсутствие по условиям договора капитализации процентов.

Это приводит к тому, что один и тот же процент, начисленный в первый период, всегда меньше, чем в последующий – ведь база для исчисления процента вырастает со временем.Такой процент называется сложным процентом.

Во вкладах и кредитах, где база для начисления процента не меняется со временем, всегда остается равной первоначальной сумме, расчет производится по формуле простых процентов.

Расчётные формулы

Для каждого вида процентов существует своя формула, помогающая её определить. Прежде чем приступать к расчётам, следует разобраться в основных терминах, которые применяются в формулах:

• Период начисления. Промежуток времени, к которому приурочена простая и сложная процентная ставка.
• Капитализация. Суммирование начисленных процентов с основной суммой задолженности.
• Наращение. Увеличение денежной суммы во времени, вызванное капитализацией.

Наращение и дисконтирование характеризуются соответствующими множителями. Первый рассчитывается как L = S (n) / S (0), второй как v = S (0) / S (n). S (0) соответствует первоначальной сумме кредита, S (n) равняется величине долга в конце срока n.

Чтобы узнать n (срок задолженности в долях от периода t), требуется разделить срок долга в днях (t) на фиксированный временной промежуток, к которому относится ставка (t*). Обычно t* равен 365 дней (иногда уменьшен до 360).

Зная необходимые параметры, можно высчитать процент (i), используя выражение i = (S (t*) — S (0)): S (0). В случае с прямыми процентами исходной базой для определения процентной ставки в течение всего срока долга на каждом периоде применения процента служит первоначальная сумма долга S (0).

На основе этих же данных можно определить значение учётной ставки по формуле d = (S (t*) — S (0)): S (t*). Учётной считается та ставка, которая используется Центробанком для предоставления заёмов коммерческим банком.

Если срок задолженности t состоит из k этапов, то чтобы при действующей схеме простых процентов узнать размер наращенного вклада по окончании срока, придётся применить выражение S (n) = S (0) * (1 + n1 * i1 + … + nk * ik).

Допустим, что в первом полугодии простой процент составляет 0,09 годовых, затем в следующем году он сокращается на 0,01, а в следующих двух полугодиях возрастает на 0,005 в каждом. Первональный взнос равен 800 у.е.

Получается, что S (0) = 800, n1 = 0,5, i1 = 0,09, n2 = 1, n3 = 0,5, n4 = 0,5. Высчитываем i2 = 0,09 — 0,01 = 0,08, i3 = 0,08 + 0,005 = 0,085, i4 = 0,085 + 0,005 = 0,09.

Подставляем полученные цифры в формулу и узнаём, что величина наращенного вклада в конце срока составит S (n) = 800 * (1 + 0,5 * 0,09 + 1 * 0,08 + 0,5 * 0,085 + 0,5 * 0,09) = 980,97.

Обзор задач и формул сложных процентов

Самая первая задача, с которой может столкнуться инвестор — «Сколько я получу денег, инвестируя»? Она решается, если известна начальная сумма и годовая процентная ставка доходности.

Для расчета используется формула сложных процентов с капитализацией:

Где:

• К — начальный капитал,
• К — результат инвестирования (финальный капитал)
• R — годовая процентная ставка
• m — период реинвестирования (в месяцах)
• n— количество периодов реинвестирования (месяцев, кварталов, лет)

Чтобы работать чисто с годовыми периодами, нужно убрать из знаменателя 12, а из числителя — m. Но я этого делать не буду, так как ПАММ-счета удобнее всего анализировать через среднемесячную доходность.

Давайте рассмотрим пару примеров.

Пример № 1. Иван Иванов положил 7000$ на депозит в банке. Сейчас средняя ставка по долларовым депозитам в Украине — в районе 9% в год. Вклад будет переоформляться каждый год в течение 10 лет. Сколько в итоге будет денег на банковском счету?

К =7000$, R = 9% в год, m = 12 месяцев, n = 10 (10 периодов по 12 месяцев)

Капитал вырос почти в три раза, несмотря на мизерную доходность по депозитам.

Впрочем, деньги на ПАММ-счетах реинвестируются автоматически и постоянно. Кроме того, гарантий стабильного годового дохода нет…

Поэтому рекомендую для расчетов сложного процента в ПАММ-счетах использовать ежемесячный реинвест.

Пример № 2. Пётр Петров вложил в ПАММ-счета 10000$. После анализа статистики выяснилось, что он может ожидать 30% чистой прибыли за год. И теперь Пётр хочет знать, каким будет размер капитала через полгода.

Вот, что получилось:

К =10000$, R = 30% в год, m = 1 месяц, n = 6 (6 периодов по 1 месяцу)

Для сравнения, без реинвестирования инвестор получил бы 11500$. То есть, на 97$ меньше, что почти не чувствуется — это всего лишь 0.97% от общего капитала.

Но давайте теперь посмотрим чуть дальше в следующем примере.

Пример № 3. Исидор Сидоров вложил в ПАММ-счета 5000$. Он собирается активно управлять портфелем и рассчитывает на 50% в год в течение 5 лет. Какой капитал получится в итоге?

Для расчета снова используется формула сложных процентов. Только теперь периодов не 6, а 60 — в 5 годах 60 месяцев. Сколько же получилось?

К =5000$, R = 50% в год, m = 1 месяц, n = 60 (60 периодов по 1 месяцу)

Без реинвестирования прибыль составила бы 50%*5=250%. Соответственно, капитал бы вырос до 35000$. А с учетом сложного процента — на целых 106 тысяч! Теперь разница ощущается очень сильно.

И чем больше проходит времени, тем сильнее разница. Теоретически, вложив сегодня 1$ в банк, уже ваши правнуки стали бы миллионерами.

Я не раз видел, как эту «фишку» используют в фильмах. Например, сюжет может быть такой:

Когда-то давно кто-то спрятал честно или нечестно заработанные деньги в скромный банк. И забыл о деньгах. Или надолго попал в тюрьму. Или умер. В общем, о деньгах забыли.

И вот, через 20-30 лет этот счет обнаруживают, а там лежат миллионы или даже миллиарды долларов. И начинается охота за паролями, поиск владельца, взлом хитромудрых защитных систем и т.д. Что придумают сценаристы 🙂

В прошлой статье я упоминал о том, что консервативные ПАММ-счета растут по параболе из-за сложного процента. Теперь вы на 100% понимаете, как это работает!

Кроме постоянного реинвестирования прибыли, инвестор может дополнительно «доливать» деньги в свой портфель. Эти деньги тоже будут приносить доход, поэтому формула сложных процентов немного усложняется.

Ну как немного… В общем, смотрите:

AI (AdditionalInvestments) — размер постоянного пополнения.

С левым слагаемым вы знакомы, а правое — расчет сложного процента по новым вложениям. Формула правильная, я проверял 🙂

Пример

Хорошей иллюстрацией является известная евангельская притча о том, как одна бедная вдова во времена Иисуса Христа принесла в жертву в храм последнее, что у неё было — две самых мелких монеты, лепты. Если представить себе, что в то время существовали банки, и она внесла бы одну монетку в банк, то какая сумма накопилась бы на банковском счёте к сегодняшнему дню, учитывая, что банк обеспечивает капитализацию процентов в сумме, скажем, пять процентов годовых?

Последующие расчёты как раз и иллюстрируют применение сложных процентов. Нам легче будет говорить, не о лепте, а о копейке. Если ставка составляет 5 % годовых, то после первого года хранения капитал составил бы копейку плюс 5 % от неё, то есть возрос бы в (1 + 0,05) раза. На второй год 5 % рассчитывались бы уже не от одной копейки, а от величины, большей её в (1 + 0,05) раза. И, в свою очередь, данная величина увеличилась бы тоже за год в (1 + 0,05) раза. Значит, по сравнению с первичной суммой вклад за два года возрос бы в раз. За три года — в раз.

К 2016 году первичный вклад вырос бы до величины в раз больше первоначальной. Величина составляет . При первоначальном вкладе в одну копейку к 2012 году сумма составит рублей, т.е. свыше 52 додециллионов.

Первоначальная идея применения к старинной притче оценок в сложных процентах принадлежит польскому математику Станиславу Ковалю и опубликована им в начале семидесятых годов в книге «500 математичных загадок».

Точная формула для оплаты ежемесячно

Точная формула для ежемесячного платежа

с = ежемесячный платеж P = начальная сумма r = ежемесячная процентная ставка n = количество периодов выплат

Периодическое начисление

Функция суммы сложных процентов является экспоненциальной функцией с точки зрения времени.

t = Общее время в годax

n = число периодов наращения в год

г = Номинальная годовая процентная ставка выражается в виде десятичной дроби. 6 т.д .:% = 0,06

nt = означает, что nt округляется до ближайшего целого числа.

Сложный процент в инвестициях

На радость инвесторам сложный процент применим не только к банковским депозитам, которые не отличаются высокими процентными ставками. Он также активно используется в инвестировании. Рассмотрим особенности расчета сложного процента при использовании разных инвестиционных инструментов.

• Облигации. Если вы предпочитаете инвестировать в старые добрые облигации, то это не мешает вам реинвестировать получаемый от них доход. Купонные выплаты по облигациям с фиксированной процентной ставкой выплачиваются раз в квартал, полугодие или год. Если сумма дохода позволяет, его можно реинвестировать, купив те же или похожие ценные бумаги. К следующему моменту выплаты доход уже немного увеличится, и если действовать по такой схеме, к окончанию срока бумаг можно получить приличный капитал.
• Акции. Реинвестирование дохода в акции происходит по аналогичной схеме. Инвестор на полученные деньги приобретает такие же ценные бумаги, увеличивая сумму следующих дивидендов. Некоторые инвесторы предпочитают вкладывать основной капитал в акции надежных эмитентов с умеренной доходностью, а при реинвестировании приобретать более рискованные ценные бумаги с высоким уровнем доходности. Это позволяет им соблюсти баланс между защитой капитала и повышением прибыли от инструмента.

Вспомогательные формул расчета сложных процентов

Из формулы, которую мы использовали раньше, можно получить несколько других, которые могут пригодиться инвестору при решении финансовых задач.

Например, иногда нужно найти не финальный, а начальный капитал.

Пример № 4. Аркадий Аркадьев интересуется, сколько ему нужно вложить денег, чтобы получить через 5 лет при ставке доходности 30% в год 100000$. Реинвест — каждый квартал.

Для этого мы используем такую формулу:

Выглядит немного страшно, но цифры точно те же, что мы использовали до этого. Подставим наши данные в формулу и найдем начальный капитал:

K = 100000$, R = 30% в год, m = 3 месяца, n = 20 (5 лет — это 20 кварталов)

Оказалось, нужно почти в 5 раз меньше. Круто, не так ли?

Идем дальше. Давайте представим ситуацию — инвестор хочет вложить деньги на определенный срок. И он рассчитывает по итогам достичь определенной суммы капитала. Какую процентную ставку ему нужно получить?

Чтобы это узнать, для расчета нам нужна формула сложных процентов для средней процентной ставки:

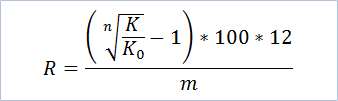
Пример № 5. Начальные инвестиции Максима Максимова — 13000$. Через два года они должны превратиться в 18000$. Реинвест ежемесячный (m= 1). Под какую ставку доходности Максиму нужно собирать инвестиционный портфель, чтобы выйти на требуемую сумму?

Подставляем числа:

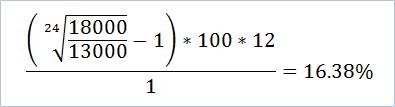
K = 18000$, К =13000$, m = 1 месяц, n = 24 (2 года = 24 месяца)

Естественно, это годовая ставка. Её можно превратить в месячную, если из числителя убрать 12, и тогда получится около 1.5% в месяц — минимальный порог для ПАММ-счетов.

Что там можно еще найти? Ах, да — сколько нужно времени, чтобы получить определенную сумму при определенной ставке. Давайте попробуем 🙂

Если в прошлом примере у нас были корни, то теперь — логарифмы. Формулы кажутся огромными, но на самом деле их легко реализовать в программе. Чтобы рассчитать сложный процент, формула Excel нужна для одной ячейки — вот и выражаем одно через все остальное. И работает это отлично!

Итак, мы будем использовать такую формулу:

Пример № 6. У Елены Лениной — 4500$, которые она хочет инвестировать. Она понимает, что может рассчитывать на 50% в год, при этом хочет достичь первой цели — 20000$. Возможно, хочет купить со временем новую машину 🙂

Через сколько времени она достигнет своей цели с условием ежемесячного реинвестирования прибыли? Подставляем числа:

K = 20000$, К =4500$, R = 50%, m = 1 месяц

Довольно быстро, должен сказать.

Кстати, опытных инвесторов часто интересует не на сколько, когда и как вырастет капитал. Их больше интересует, когда деньги удвоятся. Другими словами — через сколько они «отобьют» вложения.

Чтобы это узнать, существует универсальное «правило 72». Суть его простая — делите 72 на процентную ставку за месяц (квартал, год). Результат — это и есть тот срок, за который инвестиции удвоятся (в тех же единицах времени, что и ставка доходности).

Пример № 7. Инвестор Владимир ВладимирОвич вкладывает деньги под 10% в месяц. Через сколько он отобьет вложения?

Ответ: через 72/10=7.2 месяца.

Вложения под 6% в месяц дают удвоение капитала за год. Под 3% — за 2 года.

Послесловие

В рамках данного обзора, вы узнали что такое капитализация процента, какова формула сложных процентов, а так же увидели пример с расчетом, демонстрирующим разницу в доходе.

Хоть, сложные проценты и могут представлять интерес, всегда важно помнить про здравую логику и то, что у вас своя голова. Во-первых, могут присутствовать различные тонкости (что и когда можно снимать, что происходит если снять деньги раньше, некратные периоды и так далее)

Во-вторых, чрезмерные сложности при расчетах и сравнении, особенно если используются дробные цифры (например, 6,03% в год с ежегодной капитализацией за 10 лет составит примерно 79,6% дохода, а вот 5,96% при ежемесячной капитализации составит 81,2%). Подобные вещи непросто заметить обычному человеку.

В-третьих, капитализация предусматривает автоматическое повторное вложение денег, в то время как простые проценты могут подразумевать возможность использовать доход для иных целей. И так далее.