Метод пузырьков в информатике
Содержание:
Алгоритмы сортировки на собеседовании
Алгоритмов сортировки достаточно много, и вряд ли можно встретить программиста, который может по памяти написать реализацию хотя бы половины из них.
На самом деле, программисты просто гуглят необходимую реализацию. Конечно, они имеют представление о принципах их работы, потому что в своё время рассмотрели несколько алгоритмов, как, например, сортировка пузырьком.
Кроме того, в Python и других языках программирования существуют встроенные функции, которые производят сортировку быстро и эффективно.
На собеседованиях спрашивают про алгоритмы сортировки, но это не значит, что от будущего работника требуют написать их реализацию или придумать свой. Работодатель требует от специалиста следующее:
- Уметь классифицировать алгоритмы сортировки.
- Знать преимущества и недостатки популярных алгоритмов, чтобы понимать, когда каждый из них лучше использовать.
- Понимать, что такое сложность алгоритма и как с её помощью определять, подходит ли он для решения данной задачи.
Анализ
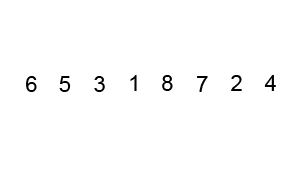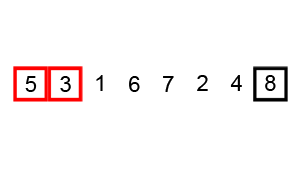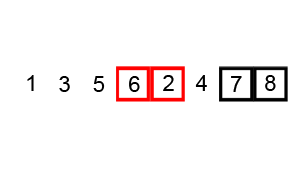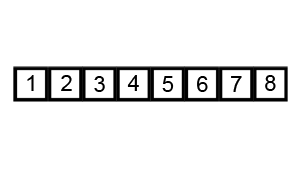
Пример пузырьковой сортировки. Начиная с начала списка, сравните каждую соседнюю пару, поменяйте их местами, если они не в правильном порядке (последняя меньше первой). После каждой итерации необходимо сравнивать на один элемент меньше (последний), пока не останется больше элементов для сравнения.
Представление
Пузырьковая сортировка имеет наихудший случай и среднюю сложность О ( n 2 ), где n — количество сортируемых элементов. Большинство практических алгоритмов сортировки имеют существенно лучшую сложность в худшем случае или в среднем, часто O ( n log n ). Даже другое О ( п 2 ) алгоритмы сортировки, такие как вставки рода , как правило , не работать быстрее , чем пузырьковой сортировки, а не более сложным. Следовательно, пузырьковая сортировка не является практическим алгоритмом сортировки.
Единственное существенное преимущество пузырьковой сортировки перед большинством других алгоритмов, даже быстрой сортировкой , но не сортировкой вставкой , заключается в том, что в алгоритм встроена способность определять, что список сортируется эффективно. Когда список уже отсортирован (в лучшем случае), сложность пузырьковой сортировки составляет всего O ( n ). Напротив, большинство других алгоритмов, даже с лучшей средней сложностью , выполняют весь процесс сортировки на множестве и, следовательно, являются более сложными. Однако сортировка вставкой не только разделяет это преимущество, но также лучше работает со списком, который существенно отсортирован (имеет небольшое количество инверсий ). Кроме того, если такое поведение желательно, его можно тривиально добавить к любому другому алгоритму, проверив список перед запуском алгоритма.
В случае больших коллекций следует избегать пузырьковой сортировки. Это не будет эффективно в случае коллекции с обратным порядком.
Кролики и черепахи
Расстояние и направление, в котором элементы должны перемещаться во время сортировки, определяют производительность пузырьковой сортировки, поскольку элементы перемещаются в разных направлениях с разной скоростью. Элемент, который должен двигаться к концу списка, может перемещаться быстро, потому что он может принимать участие в последовательных заменах. Например, самый большой элемент в списке будет выигрывать при каждом обмене, поэтому он перемещается в свою отсортированную позицию на первом проходе, даже если он начинается с начала. С другой стороны, элемент, который должен двигаться к началу списка, не может двигаться быстрее, чем один шаг за проход, поэтому элементы перемещаются к началу очень медленно. Если наименьший элемент находится в конце списка, потребуется n −1 проход, чтобы переместить его в начало. Это привело к тому, что эти типы элементов были названы кроликами и черепахами соответственно в честь персонажей басни Эзопа о Черепахе и Зайце .
Были предприняты различные попытки уничтожить черепах, чтобы повысить скорость сортировки пузырей. Сортировка коктейлей — это двунаправленная сортировка пузырьков, которая идет от начала до конца, а затем меняет свое направление, идя от конца к началу. Он может довольно хорошо перемещать черепах, но сохраняет сложность наихудшего случая O (n 2 ) . Комбинированная сортировка сравнивает элементы, разделенные большими промежутками, и может очень быстро перемещать черепах, прежде чем переходить к все меньшим и меньшим промежуткам, чтобы сгладить список. Его средняя скорость сопоставима с более быстрыми алгоритмами вроде быстрой сортировки .
Пошаговый пример
Возьмите массив чисел «5 1 4 2 8» и отсортируйте его от наименьшего числа к наибольшему, используя пузырьковую сортировку. На каждом этапе сравниваются элементы, выделенные жирным шрифтом . Потребуется три прохода;
- Первый проход
- ( 5 1 4 2 8) → ( 1 5 4 2 8). Здесь алгоритм сравнивает первые два элемента и меняет местами, поскольку 5> 1.
- (1 5 4 2 8) → (1 4 5 2 8), поменять местами, поскольку 5> 4
- (1 4 5 2 8) → (1 4 2 5 8), поменять местами, поскольку 5> 2
- (1 4 2 5 8 ) → (1 4 2 5 8 ). Теперь, поскольку эти элементы уже упорядочены (8> 5), алгоритм не меняет их местами.
- Второй проход
- ( 1 4 2 5 8) → ( 1 4 2 5 8)
- (1 4 2 5 8) → (1 2 4 5 8), поменять местами, поскольку 4> 2
- (1 2 4 5 8) → (1 2 4 5 8)
- (1 2 4 5 8 ) → (1 2 4 5 8 )
Теперь массив уже отсортирован, но алгоритм не знает, завершился ли он. Алгоритму требуется один дополнительный полный проход без какой-либо подкачки, чтобы знать, что он отсортирован.
- Третий проход
- ( 1 2 4 5 8) → ( 1 2 4 5 8)
- (1 2 4 5 8) → (1 2 4 5 8)
- (1 2 4 5 8) → (1 2 4 5 8)
- (1 2 4 5 8 ) → (1 2 4 5 8 )
Как улучшить пузырьковую сортировку
Ниже вы можете видеть оптимизированную версию пузырьковой сортировки.
for (int i = 0; i < 10; i++) {
bool flag = true;
for (int j = 0; j < 10 — (i + 1); j++) {
if (digitals > digitals) {
flag = false;
swap (digitals, digitals);
}
}
if (flag) {
break;
}
}
|
1 |
for(inti=;i<10;i++){ boolflag=true; for(intj=;j<10-(i+1);j++){ if(digitalsj>digitalsj+1){ flag=false; swap(digitalsj,digitalsj+1); } } if(flag){ break; } } |
Давайте посмотрим, что мы сделали для ее оптимизации:
- В строке 17: изменили условие внутреннего цикла на .Поэтому чтобы лишний раз не сравнивать элементы массива тратя на это время, мы решили уменьшать отрезок внутреннего цикла на 1, после каждого полного прохода внешнего цикла.
- Вы могли заметить, что если даже массив стал отсортирован (или сразу был отсортирован) алгоритм все равно продолжает сравнивать элементы.
Для этого в строке 5: чтобы пузырьковая сортировка останавливалась (когда массив уже стал отсортирован), мы объявили булеву переменную (ее обычно называют флаг или флажок). Еще при ее инициализации мы поместили значение , но она меняется на:
false, если результат условия в строке 4: положительный.
А в строке 9: чтобы мы могли выйти из алгоритма мы проверяем:
- Если булева переменная равна , значит массив уже полностью отсортирован и можно выйти. Для этого используем оператор .
- Если же значение равно , то продолжаем сортировать массив.
В строке 6: вы (возможно) увидели незнакомую функцию . Если коротко описать что она делает, то она принимает два аргумента (через запятую) и меняет их значения местами. В нашем случаи она принимает ячейки и . Мы использовали эту функцию чтобы не писать вот эти 3 строчки:
int b = digitals;
digitals = digitals;
digitals = b;
|
1 |
intb=digitalsj; digitalsj=digitalsj+1; digitalsj+1=b; |
Использовать ее необязательно, потому что она не сделает код быстрее. Но как мы сказали выше, кода станет меньше.
Разница между пузырьковой сортировкой и выборочной сортировкой
Определение
Bubble sort — простой алгоритм сортировки, который непрерывно проходит по списку и сравнивает соседние пары для сортировки элементов. Напротив, сортировка выбора — это алгоритм сортировки, который принимает наименьшее значение (с учетом возрастания) в списке и перемещает его в нужную позицию в массиве. Таким образом, в этом заключается основное различие между сортировкой пузырьков и сортировкой выбора.
функциональность
Пузырьковая сортировка сравнивает соседние элементы и соответственно меняет местами, в то время как сортировка выбора выбирает минимальный элемент из несортированного подмассива и помещает его в следующую позицию отсортированного подмассива.
КПД
Кроме того, еще одно различие между сортировкой пузырьков и сортировкой выбора заключается в том, что сортировка выбора эффективна по сравнению с сортировкой пузырьков.
скорость
Кроме того, скорость является еще одной разницей между сортировкой пузырьков и сортировкой выбора. Сортировка выбора происходит быстрее по сравнению с пузырьковой сортировкой.
метод
Кроме того, еще одно различие между пузырьковой сортировкой и сортировкой выбора заключается в том, что в пузырьковой сортировке используется обмен элементов, а в выборочной сортировке используется выбор элементов.
Заключение
Таким образом, основное различие между сортировкой пузырьков и сортировкой выбора заключается в том, что сортировка пузырьков выполняется путем многократной замены смежных элементов, если они находятся в неправильном порядке. Напротив, сортировка выбора сортирует массив путем многократного нахождения минимального элемента из несортированной части и размещения его в начале массива.
Сравнение скоростей сортировок
Для сравнения сгенерируем массив из 5000 чисел от 0 до 1000. Затем определим время, необходимое для завершения каждого алгоритма. Повторим каждый метод 10 раз, чтобы можно было более точно установить, насколько каждый из них производителен.
Пузырьковая сортировка — самый медленный из всех алгоритмов. Возможно, он будет полезен как введение в тему алгоритмов сортировки, но не подходит для практического использования.Быстрая сортировка хорошо оправдывает своё название, почти в два раза быстрее, чем сортировка слиянием, и не требуется дополнительное место для результирующего массива.Сортировка вставками выполняет меньше сравнений, чем сортировка выборкой и в реальности должна быть производительнее, но в данном эксперименте она выполняется немного медленней. Сортировка вставками делает гораздо больше обменов элементами. Если эти обмены занимают намного больше времени, чем сравнение самих элементов, то такой результат вполне закономерен.
Вы познакомились с шестью различными алгоритмами сортировок и их реализациями на Python. Масштаб сравнения и количество перестановок, которые выполняет алгоритм вместе со средой выполнения кода, будут определяющими факторами в производительности. В реальных приложениях Python рекомендуется использовать встроенные функции сортировки, поскольку они реализованы именно для удобства разработчика.
Лучше понять эти алгоритмы вам поможет их визуализация.
Перевод статьи «Sorting Algorithms in Python»
Модификации[править]
Сортировка чет-нечетправить
Сортировка чет-нечет (англ. odd-even sort) — модификация пузырьковой сортировки, основанная на сравнении элементов стоящих на четных и нечетных позициях независимо друг от друга. Сложность — .
Псевдокод указан ниже:
function oddEvenSort(a):
for i = 0 to n - 1
if i mod 2 == 0
for j = 2 to n - 1 step 2
if a < a
swap(a, a)
else
for j = 1 to n - 1 step 2
if a < a
swap(a, a)
Преимущество этой сортировки — на нескольких процессорах она выполняется быстрее, так как четные и нечетные индексы сортируются параллельно.
Сортировка расческойправить
Сортировка расческой (англ. comb sort) — модификация пузырьковой сортировки, основанной на сравнении элементов на расстоянии. Сложность — , но стремится к . Является самой быстрой квадратичной сортировкой. Недостаток — она неустойчива. Псевдокод указан ниже:
function combSort(a):
k = 1.3
jump = n
bool swapped = true
while jump > 1 and swapped
if jump > 1
jump /= k
swapped = false
for i = 0 to size - jump - 1
if a < a
swap(a, a)
swapped = true
Пояснения: Изначально расстояние между сравниваемыми элементами равно , где — оптимальное число для этого алгоритма. Сортируем массив по этому расстоянию, потом уменьшаем его по этому же правилу. Когда расстояние между сравниваемыми элементами достигает единицы, массив досортировывается обычным пузырьком.
Сортировка перемешиваниемправить
Сортировка перемешиванием (англ. cocktail sort), также известная как Шейкерная сортировка — разновидность пузырьковой сортировки, сортирующая массив в двух направлениях на каждой итерации. В среднем, сортировка перемешиванием работает в два раза быстрее пузырька. Сложность — , но стремится она к , где — максимальное расстояние элемента в неотсортированном массиве от его позиции в отсортированном массиве. Псевдокод указан ниже:
function shakerSort(a):
begin = -1
end = n - 2
while swapped
swapped = false
begin++
for i = begin to end
if a > a
swap(a, a)
swapped = true
if !swapped
break
swapped = false
end--
for i = end downto begin
if a > a
swap(a, a)
swapped = true
Основы сортировки
Для сортировки по возрастанию достаточно вызвать функцию сортировки Python , которая вернёт новый отсортированный список:
Также можно использовать метод списков , который изменяет исходный список (и возвращает во избежание путаницы). Обычно это не так удобно, как использование , но если вам не нужен исходный список, то так будет немного эффективнее:
Прим.перев. В Python вернуть и не вернуть ничего — одно и то же.
Ещё одно отличие заключается в том, что метод определён только для списков, в то время как работает со всеми итерируемыми объектами:
Прим.перев. При итерировании по словарю Python возвращает его ключи. Если вам нужны их значения или пары «ключ-значение», используйте методы и соответственно.
Рассмотрим основные функции сортировки Python.
2
Сортировка многомерного массива
Сортировка статического многомерного массива по существу не отличается от сортировки одномерного. Можно воспользоваться тем свойством, что статический одномерный и многомерный массивы имеют одинаковое представление в памяти.
void main() {
int a = {1, 9, 2, 8, 3, 7, 4, 6, 5};
int i, j;
bubbleSort3gi(a, sizeof(int), 9, intSort);
for (i = 0; i < 3; i++) {
for (j = 0; j < 3; j++) {
printf("%d ", a);
}
}
}
#include <conio.h>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
void bubbleSort2d(int **a, size_t m, size_t n) {
int tmp;
size_t i, j, k, jp, ip;
size_t size = m*n;
char flag;
do {
flag = 0;
for (k = 1; k < size; k++) {
//Вычисляем индексы текущего элемента
j = k / m;
i = k - j*m;
//Вычисляем индексы предыдущего элемента
jp = (k-1) / m;
ip = (k-1) - jp*m;
if (a > a) {
tmp = a;
a = a;
a = tmp;
flag = 1;
}
}
} while(flag);
}
#define SIZE_X 3
#define SIZE_Y 4
void main() {
int **a = NULL;
int i, j;
a = (int**) malloc(sizeof(int*) * SIZE_X);
for (i = 0; i < SIZE_X; i++) {
a = (int*) malloc(sizeof(int) * SIZE_Y);
for (j = 0; j < SIZE_Y; j++) {
a = rand();
printf("%8d ", a);
}
printf("\n");
}
printf("\nafter sort\n");
bubbleSort2d(a, SIZE_X, SIZE_Y);
for (i = 0; i < SIZE_X; i++) {
for (j = 0; j < SIZE_Y; j++) {
printf("%8d ", a);
}
printf("\n");
}
for (i = 0; i < SIZE_X; i++) {
free(a);
}
free(a);
_getch();
}
Во-вторых, можно сначала переместить массив в одномерный, отсортировать одномерный массив, после чего переместить его обратно в двумерный.
void bubbleSort3gi2d(void **a, size_t item, size_t m, size_t n, int (*cmp)(const void*, const void*)) {
size_t size = m*n, sub_size = n*item;
size_t i, j, k;
void *arr = malloc(size * item);
char *p1d = (char*)arr;
char *p2d = (char*)a;
//Копируем двумерный массив типа void в одномерный
for (i = 0; i < m; i++) {
memcpy(p1d + i*sub_size, *((void**)(p2d + i*item)), sub_size);
}
bubbleSort3gi(arr, item, size, cmp);
//Копируем одномерный массив обратно в двумерный
for (i = 0; i < m; i++) {
memcpy(*((void**)(p2d + i*item)), p1d + i*sub_size, sub_size);
}
}
Если вас смущает эта функция, то воспользуйтесь типизированной. Вызов, из предыдущего примера
bubbleSort3gi2d((void**)a, sizeof(int), SIZE_X, SIZE_Y, intSort);
Q&A
Всё ещё не понятно? – пиши вопросы на ящик
Complexity Analysis of Bubble Sort
In Bubble Sort, comparisons will be done in the 1st pass, in 2nd pass, in 3rd pass and so on. So the total number of comparisons will be,
(n-1) + (n-2) + (n-3) + ….. + 3 + 2 + 1
Sum = n(n-1)/2
i.e O(n2)
Hence the time complexity of Bubble Sort is O(n2).
The main advantage of Bubble Sort is the simplicity of the algorithm.
The space complexity for Bubble Sort is O(1), because only a single additional memory space is required i.e. for variable.
Also, the best case time complexity will be O(n), it is when the list is already sorted.
Following are the Time and Space complexity for the Bubble Sort algorithm.
- Worst Case Time Complexity : O(n2)
- Best Case Time Complexity : O(n)
- Average Time Complexity : O(n2)
- Space Complexity: O(1)
Now that we have learned Bubble sort algorithm, you can check out these sorting algorithms and their applications as well:
Сортировка пузырьком
Идея алгоритма очень простая. Идём по массиву чисел и проверяем порядок (следующее число должно быть больше и равно предыдущему), как только наткнулись на нарушение порядка, тут же обмениваем местами элементы, доходим до конца массива, после чего начинаем сначала.
Отсортируем массив {1, 5, 2, 7, 6, 3}
Идём по массиву, проверяем первое число и второе, они идут в порядке возрастания. Далее идёт нарушение порядка, меняем местами эти элементы
Продолжаем идти по массиву, 7 больше 5, а вот 6 меньше, так что обмениваем из местами
3 нарушает порядок, меняем местами с 7
Возвращаемся к началу массива и проделываем то же самое
void bubbleSort(int *a, size_t size) {
size_t i, j;
int tmp;
for (i = 1; i < size; i++) {
for (j = 1; j < size; j++) {
if (a > a) {
tmp = a;
a = a;
a = tmp;
}
}
}
}
Этот алгоритм всегда будет делать (n-1)2 шагов, независимо от входных данных. Даже если массив отсортирован, всё равно он будет пройден (n-1)2 раз. Более того, будут в очередной раз проверены уже отсортированные данные.
Пусть нужно отсортировать массив 1, 2, 4, 3
После того, как были поменяны местами элемента a и a нет больше необходимости проходить этот участок массива
Примем это во внимание и переделаем алгоритм
void bubbleSort2(int *a, size_t size) {
size_t i, j;
int tmp;
for (i = 1; i < size; i++) {
for (j = i; j > 0; j--) {
if (a < a) {
tmp = a;
a = a;
a = tmp;
}
}
}
}
Ещё одна реализация
void bubbleSort2b(int *a, size_t size) {
size_t i, j;
int tmp;
for (i = 1; i < size; i++) {
for (j = 1; j <= size-i; j++) {
if (a < a) {
tmp = a;
a = a;
a = tmp;
}
}
}
}
В данном случае будет уже вполовину меньше шагов, но всё равно остаётся проблема сортировки уже отсортированного массива: нужно сделать так, чтобы отсортированный массив функция просматривала один раз. Для этого введём переменную-флаг: он будет опущен (flag = 0), если массив отсортирован. Как только мы наткнёмся на нарушение порядка, то флаг будет поднят (flag = 1) и мы начнём сортировать массив как обычно.
void bubbleSort3(int *a, size_t size) {
size_t i;
int tmp;
char flag;
do {
flag = 0;
for (i = 1; i < size; i++) {
if (a < a) {
tmp = a;
a = a;
a = tmp;
flag = 1;
}
}
} while (flag);
}
В этом случае сложность также порядка n2, но в случае отсортированного массива будет всего один проход.
Теперь усовершенствуем алгоритм. Напишем функцию общего вида, чтобы она сортировала массив типа void. Так как тип переменной не известен, то нужно будет дополнительно передавать размер одного элемента массива и функцию сравнения.
int intSort(const void *a, const void *b) {
return *((int*)a) > *((int*)b);
}
void bubbleSort3g(void *a, size_t item, size_t size, int (*cmp)(const void*, const void*)) {
size_t i;
void *tmp = NULL;
char flag;
tmp = malloc(item);
do {
flag = 0;
for (i = 1; i < size; i++) {
if (cmp(((char*)a + i*item), ((char*)a + (i-1)*item))) {
memcpy(tmp, ((char*)a + i*item), item);
memcpy(((char*)a + i*item), ((char*)a + (i-1)*item), item);
memcpy(((char*)a + (i-1)*item), tmp, item);
flag = 1;
}
}
} while (flag);
free(tmp);
}
Функция выглядит некрасиво – часто вычисляется адрес текущего и предыдущего элемента. Выделим отдельные переменные для этого.
void bubbleSort3gi(void *a, size_t item, size_t size, int (*cmp)(const void*, const void*)) {
size_t i;
void *tmp = NULL;
void *prev, *cur;
char flag;
tmp = malloc(item);
do {
flag = 0;
i = 1;
prev = (char*)a;
cur = (char*)prev + item;
while (i < size) {
if (cmp(cur, prev)) {
memcpy(tmp, prev, item);
memcpy(prev, cur, item);
memcpy(cur, tmp, item);
flag = 1;
}
i++;
prev = (char*)prev + item;
cur = (char*)cur + item;
}
} while (flag);
free(tmp);
}
Теперь с помощью этих функций можно сортировать массивы любого типа, например
void main() {
int a = {1, 0, 9, 8, 7, 6, 2, 3, 4, 5};
int i;
bubbleSort3gi(a, sizeof(int), 10, intSort);
for (i = 0; i < 10; i++) {
printf("%d ", a);
}
_getch();
}
Pseudocode
We observe in algorithm that Bubble Sort compares each pair of array element unless the whole array is completely sorted in an ascending order. This may cause a few complexity issues like what if the array needs no more swapping as all the elements are already ascending.
To ease-out the issue, we use one flag variable swapped which will help us see if any swap has happened or not. If no swap has occurred, i.e. the array requires no more processing to be sorted, it will come out of the loop.
Pseudocode of BubbleSort algorithm can be written as follows −
procedure bubbleSort( list : array of items )
loop = list.count;
for i = 0 to loop-1 do:
swapped = false
for j = 0 to loop-1 do:
/* compare the adjacent elements */
if list > list then
/* swap them */
swap( list, list )
swapped = true
end if
end for
/*if no number was swapped that means
array is sorted now, break the loop.*/
if(not swapped) then
break
end if
end for
end procedure return list
Bubble sort program in C
/* Bubble sort code */
#include <stdio.h>
int main(){ int array100, n, c, d, swap;
printf(«Enter number of elements\n»); scanf(«%d», &n);
printf(«Enter %d integers\n», n);
for (c = ; c < n; c++) scanf(«%d», &arrayc);
for (c = ; c < n — 1; c++) { for (d = ; d < n — c — 1; d++) { if (arrayd > arrayd+1) /* For decreasing order use ‘<‘ instead of ‘>’ */ { swap = arrayd; arrayd = arrayd+1; arrayd+1 = swap; } } }
printf(«Sorted list in ascending order:\n»);
for (c = ; c < n; c++) printf(«%d\n», arrayc);
return ;}
Output of program: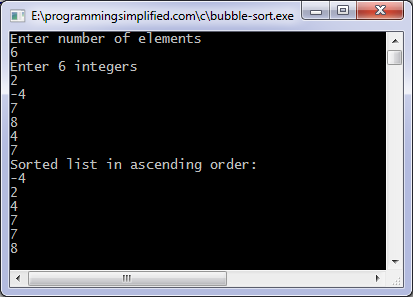
Download Bubble sort program.
Other sorting algorithms:Selection sort in CInsertion sort in C
There are many fast sorting algorithms like Quicksort, heap-sort, and others. Sorting simplifies problem-solving in computer programming.
Conclusion
Bubble sort is a fairly simple algorithm. It forms an interesting example of how simple computations can be used to perform more complex tasks. However, there is one issue with the algorithm — it is relatively slower compared to other sorting algorithms. To understand that, let us take a look at the loops involved — there are 2 loops:
- First, the outer loop of variable i that goes from i = 0 to i = n — 1.
- For each iteration of the outer i loop, the inner loop of variable j goes from j = 0 to j = n — i — 2.
We can consolidate the number of iterations to see that:
- When i = 0, the inner j loop goes from j = 0 to j = n — 2
- When i = 1, the inner j loop goes from j = 0 to j = n — 3
- When i = 2, the inner j loop goes from j = 0 to j = n — 4
- When i = n — 2, the inner j loop goes from j = 0 to j = 0
We can sum this up to see that the total iterations are (n — 2) + (n — 3) + (n — 4) … + 1 + 0 = (n — 2) * (n — 3) / 2 = (n2 — 5n + 6) / 2 = n2/2 — 2.5n + 3As can be seen, this term is proportional to n2 (the largest power of n is n2). Mathematically, this is stated as — bubble sort algorithm is of O(n2) complexity. This isn’t the best because when n is large (say n = 106), n2 is huge (n2 = 1012). Therefore, it will take a lot of iterations for the algorithm to complete. This is undesirable. There are some better algorithms like merge sort in C, etc that take O(nlog2n) iterations. logn is much smaller than n. As an example, when n = 230 (which is approximately 109), log2n is just 30). Nevertheless, bubble sort is an interesting algorithm and is a great way for beginners to understand how sorting works.
People are also reading:
Analysis
There are outer iterations needed to sort the array, because every iteration puts one element to it’s place. Every inner iteration needs one step less the previous one, since the problem size is gradually decreasing.
Last part of the algorithm is a condition, which decides whether we should swap the adjacent elements.
Complexity
The complexity of the condition (and possible swap) is obviously constant (). The inner cycle will be performed
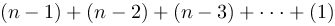
times.
Which is in total (according to the formula for arithmetic sequence):
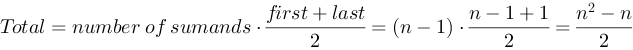
Because this number represents the best and the worst case of algorithm behavior, it’s asymptotic complexity after omitting additive and multiplicative constants is .
Вывод:
Shell sort не использует стек вызовов, и поскольку он может быть использован очень мало кода, он используется в некоторых библиотеках, таких как uClibc. Сортировка оболочки также присутствует в ядре Linux. Производительность сортировки оболочки лучше, чем сортировка вставки. Однако его href=»https://en.wikipedia.org/wiki/Cache_(вычисление)»>cache miss ratio выше, чем у quicksort. href=»https://en.wikipedia.org/wiki/Cache_(вычисление)»>cache miss ratio выше, чем у quicksort.
Однако, если у вас есть какие-либо сомнения или вопросы, дайте мне знать в разделе комментариев ниже. Я постараюсь помочь вам как можно скорее.
Счастливого Пифонирования!