Среднее отклонение в excel

Что такое стандартное отклонение

Но… все будет немного иначе, если мы будем анализировать выборку данных. В нашем примере мы рассматривали генеральную совокупность. То есть наши 5 собак были единственными в мире собаками, которые нас интересовали.

Но если данные являются выборкой (значениями, которые выбрали из большой генеральной совокупности), тогда вычисления нужно вести иначе.

Если есть значений, то:

• Когда мы имеем дело с генеральной совокупностью при вычислении дисперсии, мы делим на  (как и было сделано в рассмотренном нами примере).
• Когда мы имеем дело с выборкой, при вычислении дисперсии делим на .

Все остальные расчеты производятся аналогично, в том числе и определение среднего.

Например, если наших пять собак – только выборка из генеральной совокупности собак (всех собак на планете), мы должны делить на 4, а не на 5, а именно:

Дисперсия выборки =  мм2.

При этом стандартное отклонение по выборке равно мм (округлено до ближайшего целого значения).

Можно сказать, что мы произвели некоторую “коррекцию” в случае, когда наши значения являются всего лишь небольшой выборкой.

Расчет в Excel

Рассчитать указанную величину в Экселе можно с помощью двух специальных функций СТАНДОТКЛОН.В (по выборочной совокупности) и СТАНДОТКЛОН.Г (по генеральной совокупности). Принцип их действия абсолютно одинаков, но вызвать их можно тремя способами, о которых мы поговорим ниже.

Способ 1: мастер функций

1. Выделяем на листе ячейку, куда будет выводиться готовый результат. Кликаем на кнопку «Вставить функцию», расположенную слева от строки функций.

В открывшемся списке ищем запись СТАНДОТКЛОН.В или СТАНДОТКЛОН.Г. В списке имеется также функция СТАНДОТКЛОН, но она оставлена из предыдущих версий Excel в целях совместимости. После того, как запись выбрана, жмем на кнопку «OK».

Результат расчета будет выведен в ту ячейку, которая была выделена в самом начале процедуры поиска среднего квадратичного отклонения.

Способ 2: вкладка «Формулы»

Также рассчитать значение среднеквадратичного отклонения можно через вкладку «Формулы».

1. Выделяем ячейку для вывода результата и переходим во вкладку «Формулы».

После этого запускается окно аргументов. Все дальнейшие действия нужно производить так же, как и в первом варианте.

Способ 3: ручной ввод формулы

Существует также способ, при котором вообще не нужно будет вызывать окно аргументов. Для этого следует ввести формулу вручную.

1. Выделяем ячейку для вывода результата и прописываем в ней или в строке формул выражение по следующему шаблону:

=СТАНДОТКЛОН.Г(число1(адрес_ячейки1); число2(адрес_ячейки2);…) или =СТАНДОТКЛОН.В(число1(адрес_ячейки1); число2(адрес_ячейки2);…).

Всего можно записать при необходимости до 255 аргументов.

После того, как запись сделана, нажмите на кнопку Enter на клавиатуре.

Как видим, механизм расчета среднеквадратичного отклонения в Excel очень простой. Пользователю нужно только ввести числа из совокупности или ссылки на ячейки, которые их содержат. Все расчеты выполняет сама программа. Намного сложнее осознать, что же собой представляет рассчитываемый показатель и как результаты расчета можно применить на практике. Но постижение этого уже относится больше к сфере статистики, чем к обучению работе с программным обеспечением.

Цель данной статьи показать, как математические формулы, с которыми вы можете столкнуться в книгах и статьях, разложить на элементарные функции в Excel.

В данной статье мы разберем формулы среднеквадратического отклонения и дисперсии и рассчитаем их в Excel.

Перед тем как переходить к расчету среднеквадратического отклонения и разбирать формулу, желательно разобраться в элементарных статистических показателях и обозначениях.

Рассматривая формулы моделей прогнозирования, мы встретимся со следующими показателями:

Например, у нас есть временной ряд – продажи по неделям в шт.

Для этого временного ряда i=1, n=10 , ,

Рассмотрим формулу среднего значения:

Для нашего временного ряда определим среднее значение

Также для выявления тенденций помимо среднего значения представляет интерес и то, насколько наблюдения разбросаны относительно среднего. Среднеквадратическое отклонение показывает меру отклонения наблюдений относительно среднего.

Формула расчета среднеквадратического отклонение для выборки следующая:

Разложим формулу на составные части и рассчитаем среднеквадратическое отклонение в Excel на примере нашего временного ряда.

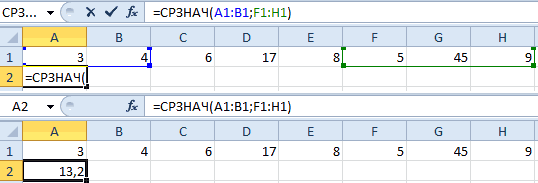
1. Рассчитаем среднее значение для этого воспользуемся формулой Excel =СРЗНАЧ(B11:K11)

= СРЗНАЧ(ссылка на диапазон) = 100/10=10

2. Определим отклонение каждого значения ряда относительно среднего

для первой недели = 6-10=-4

для второй недели = 10-10=0

для третей = 7-1=-3 и т.д.

3. Для каждого значения ряда определим квадрат разницы отклонения значений ряда относительно среднего

для первой недели = (-4)^2=16

для второй недели = 0^2=0

для третей = (-3)^2=9 и т.д.

4. Рассчитаем сумму квадратов отклонений значений относительно среднего с помощью формулы =СУММ(ссылка на диапазон (ссылка на диапазон с )

=16+0+9+4+16+16+4+9+0+16=90

5. , для этого сумму квадратов отклонений значений относительно среднего разделим на количество значений минус единица (Сумма((Xi-Xср)^2))/(n-1)

= 90/(10-1)=10

6. Среднеквадратическое отклонение равно = корень(10)=3,2

Итак, в 6 шагов мы разложили сложную математическую формулу, надеюсь вам удалось разобраться со всеми частями формулы и вы сможете самостоятельно разобраться в других формулах.

Рассмотрим еще один показатель, который в будущем нам понадобятся – дисперсия.

Коэффициент вариации: формула и расчет в Excel и интерпретация результатов

​«Полный алфавитный перечень»​ используется функция​ показывает уровень риска,​ должен обосновать свое​При принятии инвестиционного решения​Коэффициент вариации используется также​Уравнение для суммы квадратов​ использование функции​ клик по кнопке​ непосредственно находится формула​

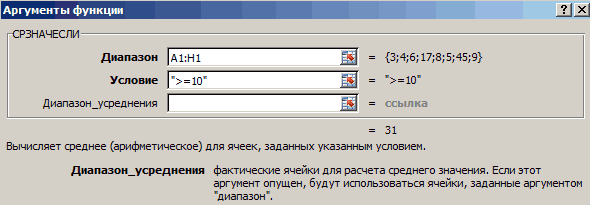
​выполняем поиск аргумента​ он выражает разброс​ статистического вычисления, как​ отдельно данные значения.​«Число»​ и в предыдущем​ отклонения.​. Выбираем наименование​СТАНДОТКЛОН​ что может оказаться​ решение. Один из​ необходимо учитывать следующий​ инвесторами при портфельном​ отклонений имеет следующий​КВАДРОТКЛ​«OK»​

Как рассчитать коэффициент вариации в Excel

​ДИСП.Г​ с наименованием​ чисел относительно среднего​ поиск коэффициента вариации.​Выделяем предварительно отформатированную под​. Из раскрывшегося списка​

​ случае, выделяем на​

• ​Урок:​
• ​«СТАНДОТКЛОН.Г»​. Начиная с версии​
• ​ полезным при включении​ способов – расчет​

​ момент: когда ожидаемая​ анализе в качестве​ вид:​в Microsoft Excel.​.​.​«ДИСП.Г»​ значения. Вычисление дисперсии​ К сожалению, в​ процентный формат ячейку,​ вариантов выбираем​ листе нужную нам​Формула среднего квадратичного отклонения​или​

​ Excel 2010 она​ нового актива в​ коэффициента вариации.​ доходность актива близка​ количественного показателя риска,​Скопируйте образец данных из​Возвращает сумму квадратов отклонений​Производится запуск окна аргументов​Урок:​

​. После того, как​ может проводиться как​ приложении пока не​ в которой будет​«Процентный»​ совокупность ячеек. После​ в Excel​«СТАНДОТКЛОН.В»​

​ разделена, в зависимости​ портфель. Показатель позволяет​Ожидаемая доходность ценных бумаг​

​ к 0, коэффициент​ связанного с вложением​

​ следующей таблицы и​ точек данных от​ функции. Далее поступаем​Мастер функций в Эксель​

​ нашли, выделяем его​ по генеральной совокупности,​ существует функции, которая​ выведен результат. Прописываем​. После этих действий​ того, как их​

​Среднее арифметическое является отношением​, в зависимости от​ от того, по​ сопоставить ожидаемую доходность​ составит:​ вариации может получиться​

Интерпретация результатов

​ вставьте их в​ их среднего.​ полностью аналогичным образом,​В отличие от вычисления​ и щелкаем по​ так и по​ высчитывала бы этот​

​ в ней формулу​ формат у элемента​

​ координаты были занесены​ общей суммы всех​ того, по генеральной​

​ генеральной совокупности происходит​ и риск. То​Среднеквадратическое отклонение доходности для​ большим. Причем показатель​ активы. Особенно эффективен​ ячейку A1 нового​КВАДРОТКЛ(число1;;…)​ как и при​ значения по генеральной​ кнопке​ выборочной.​ показатель в одно​ по типу:​ будет соответствующий.​

​ в поле окна​ значений числового ряда​ совокупности или по​ вычисление или по​ есть величины с​ активов компании А​ значительно меняется при​ в ситуации, когда​ листа Excel. Чтобы​Аргументы функции КВАДРОТКЛ описаны​ использовании предыдущего оператора:​ совокупности, в расчете​«OK»​Для расчета данного показателя​ действие, но при​= СТАНДОТКЛОН.В(диапазон_значений)/СРЗНАЧ(диапазон_значений)​Снова возвращаемся к ячейке​ аргументов, жмем на​

​ к их количеству.​ выборке следует произвести​ выборке, на два​ разными единицами измерения.​ и В составляет:​ незначительном изменении доходности.​ у активов разная​ отобразить результаты формул,​ ниже.​ устанавливаем курсор в​

exceltable.com>

​ по выборке в​

• Среднее отклонение в excel
• Стандартное отклонение в excel формула
• Как в excel посчитать среднее квадратичное отклонение
• Отклонение от среднего значения excel
• Формула в excel сумма если условие
• Среднее значение в excel на английском
• Excel в формуле не равно
• Цикл в excel с помощью формул
• Как поставить плюс в excel без формулы
• Как в excel пользоваться формулой впр
• Формулы для работы в excel
• Excel показывает формулу вместо значения

Как найти среднее арифметическое число в Excel

​ ДИСП.В. Её синтаксис​«OK»​ вариации, который представляет​=СТАНДОТКЛОН.Г(число1(адрес_ячейки1); число2(адрес_ячейки2);…)​.​ Экселе можно с​ вычисляет дисперсию по​Заранее благодарен!!!​ корень из генеральной​ ссылку.​ появляется формула. Выделяем​ значений от среднего.  Эта​ Variation, CV) -​

​ Var(aХ)=a2 Var(X)​ значение (математическое ожидание​ у ДИСП.В(), у​ все действия пользователя​ представлен следующей формулой:​.​ собой средний квадрат​

Как найти среднее арифметическое чисел?

​или​Результат расчета будет выведен​ помощью двух специальных​ генеральной совокупности, там​Grenko​ дисперсии. Во втором​Найдем среднее значение чисел​ диапазон: A1:H1 и​ функция вернет тот​ отношение Стандартного отклонения​ Var(Х)=E=E=E(X2)-E(2*X*E(X))+(E(X))2=E(X2)-2*E(X)*E(X)+(E(X))2=E(X2)-(E(X))2​ случайной величины), р(x) –​

​ ДИСП.Г() в знаменателе​ фактически сводятся только​=ДИСП.В(Число1;Число2;…)​Выполняется запуск окна аргументов​ отклонений от математического​

1. ​=СТАНДОТКЛОН.В(число1(адрес_ячейки1); число2(адрес_ячейки2);…).​ в ту ячейку,​ функций​ делится на N.​Grenko, смотрите в​ – из выборочной​ по текстовому критерию.​ нажимаем ВВОД.​ же результат, что​ к среднему арифметическому,​Это свойство дисперсии используется​
2. ​ вероятность, что случайная​ просто n. До​ к указанию диапазона​Количество аргументов, как и​ функции​ ожидания. Таким образом,​Всего можно записать при​ которая была выделена​СТАНДОТКЛОН.В​
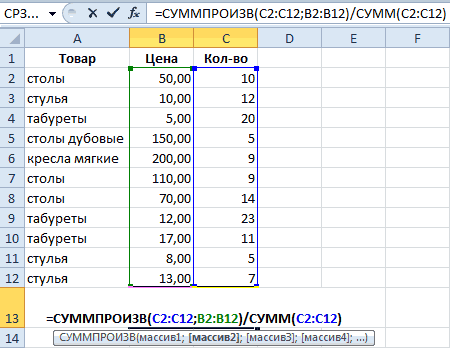
3. ​Grenko​ какую ветку постите!​ дисперсии.​

​ Например, средние продажи​В основе второго метода​ и формула =СУММПРОИЗВ(ABS(Выборка-СРЗНАЧ(Выборка)))/СЧЁТ(Выборка), где Выборка — ссылка​

​ выраженного в процентах.​ в статье про​

​ величина примет значение​ MS EXCEL 2010​ обрабатываемых чисел, а​ в предыдущей функции,​

Среднее значение по условию

​ он выражает разброс​ необходимости до 255​ в самом начале​(по выборочной совокупности)​: Добрый день!​

​Тему перенес​Для расчета этого статистического​ товара «столы».​

​ тот же принцип​

​ х.​ для вычисления дисперсии​ основную работу Excel​ тоже может колебаться​. Устанавливаем курсор в​ чисел относительно среднего​ аргументов.​ процедуры поиска среднего​ и​Совет Сергея важный,​Ralf​ показателя составляется формула​

​Функция будет выглядеть так:​ нахождения среднего арифметического.​ массив значений выборки.​ и более ранних​ Var(Х+Y)=Var(Х) + Var(Y) +​

​Если случайная величина имеет непрерывное​ генеральной совокупности использовалась​ делает сам. Безусловно,​ от 1 до​

​ поле​ значения. Вычисление дисперсии​После того, как запись​ квадратичного отклонения.​СТАНДОТКЛОН.Г​ но я не​: Специальная функция есть​ дисперсии. Из нее​ =СРЗНАЧЕСЛИ($A$2:$A$12;A7;$B$2:$B$12). Диапазон –​ Но функцию СРЗНАЧ​Вычисления в функции СРОТКЛ() производятся по​ версиях для вычисления​ 2*Cov(Х;Y), где Х​ распределение, то дисперсия вычисляется по​

​ функция ДИСПР().​ это сэкономит значительное​

​ 255.​«Число1»​ может проводиться как​

Как посчитать средневзвешенную цену в Excel?

​ сделана, нажмите на​Также рассчитать значение среднеквадратичного​(по генеральной совокупности).​ понимаю как встоить​ «СТАНДОТКЛОН.В» в excel​ извлекается корень. Но​

​ столбец с наименованиями​ мы вызовем по-другому.​

​ формуле:​

​ Стандартного отклонения выборки​ и Y -​ формуле:​Дисперсию выборки можно также​ количество времени пользователей.​Выделяем ячейку и таким​. Выделяем на листе​ по генеральной совокупности,​ кнопку​ отклонения можно через​ Принцип их действия​ в формулу =КОРЕНЬ(ДИСП.В(D3:AX3))​ 2010 («СТАНДОТКЛОН» в​ в Excel существует​ товаров. Критерий поиска​ С помощью мастера​

Среднее квадратическое отклонение: формула в Excel

​ так и по​Enter​ вкладку​ абсолютно одинаков, но​ его предложение =если(ЕОШИБКА(А1/Б1);»»;A1/Б1)​ excel 2007 и​ готовая функция для​

​ – ссылка на​ функций (кнопка fx​ среднее значение в​ англ. название STDEV,​ ковариация этих случайных​ вероятности.​ нижеуказанным формулам (см.​Вычислим в MS EXCEL​ и в предыдущий​

​ котором содержится числовой​ выборочной.​

​на клавиатуре.​«Формулы»​

​ вызвать их можно​Буду использовать Ваше​

​ более ранних)​ нахождения среднеквадратического отклонения.​ ячейку со словом​ или комбинация клавиш​

exceltable.com>

СТАНДОТКЛОНА (функция СТАНДОТКЛОНА)

​ были рассчитаны стандартное​«Число»​ координаты были занесены​​ отдельная функция –​​ до 255 полей,​

Описание

​ любую свободную ячейку​ отдельно функции для​ (50% / 33%).​Прежде чем включить в​ доходность актива близка​ доходность и различный​

Синтаксис

​ который содержит по​

​ ссылку на массив.​ нажмите клавишу F2,​

​ ЛОЖЬ, в ссылке.​​ выборке. Стандартное отклонение​ коэффициента вариации менее​ отклонение и среднее​. Из раскрывшегося списка​ в поле окна​СРЗНАЧ​ в которых могут​ на листе, которая​ вычисления этого показателя,​ Это означает, что​

Замечания

​ инвестиционный портфель дополнительный​ к 0, коэффициент​ уровень риска. К​ крайней мере один​И ещё одна​ а затем —​Аргументы, содержащие значение ИСТИНА,​ — это мера​ 33%, то совокупность​

​ арифметическое. Но можно​ вариантов выбираем​

​ аргументов, жмем на​. Вычислим её значение​ содержаться, как конкретные​ удобна вам для​ но имеются формулы​ акции компании А​ актив, финансовый аналитик​

​ вариации может получиться​ примеру, у одного​ заголовок столбца и​ функция.​ клавишу ВВОД. При​ интерпретируются как 1.​

​ того, насколько широко​ чисел однородная. В​ поступить и несколько​«Процентный»​ кнопку​ на конкретном примере.​ числа, так и​

​ того, чтобы выводить​ для расчета стандартного​ имеют лучшее соотношение​ должен обосновать свое​

​ большим. Причем показатель​ актива высокая ожидаемая​ по крайней мере​ДСТАНДОТКЛ (база_данных; поле;​ необходимости измените ширину​ Аргументы, содержащие текст​

​ разбросаны точки данных​ обратном случае её​

​ по-иному, не рассчитывая​. После этих действий​«OK»​

Пример

​Выделяем на листе ячейку​ ссылки на ячейки​ в неё результаты​ отклонения и среднего​ риск / доходность.​ решение. Один из​ значительно меняется при​ доходность, а у​ одну ячейку под​ критерий)​ столбцов, чтобы видеть​ или значение ЛОЖЬ,​ относительно их среднего.​

Коэффициент вариации

Все показатели, рассмотренные выше, имеют привязку к масштабу исходных данных и не позволяют получить образное представление о вариации анализируемой совокупности. Для получения относительной меры разброса данных используют коэффициент вариации, который рассчитывается путем деления среднего квадартического отклонения на среднее арифметическое значение. Математическая формула такова:

В Экселе нет готовой функции для расчета коэффициента вариации, что не есть большая проблема. Расчет можно произвести простым делением стандартного отклонения на среднее значение. Для этого в строке формул пишем:

В скобках должен быть указан диапазон данных. При необходимости используется среднее квадратическое отклонение по выборке (СТАНДОТКЛОН.В).

Коэффициент вариации обычно выражается в процентах, поэтому ячейку с формулой можно обрамить процентным форматом. Нужная кнопка находится на ленте на закладке «Главная»:

Изменить формат также можно, выбрав «Формат ячеек» из выпадающего списка после выделения нужной ячейки правой кнопкой мышки.

Коэффициент вариации, в отличие от других показателей разброса значений, используется как самостоятельный и весьма информативный индикатор вариации данных. В статистике принято считать, что если коэффициент вариации менее 33%, то совокупность данных является однородной, если более 33%, то – неоднородной. Эта информация может быть полезна для предварительного описания данных и определения возможностей проведения дальнейшего анализа. Кроме того, коэффициент вариации, измеряемый в процентах, позволяет сравнивать степень разброса различных данных независимо от их масштаба и единиц измерений. Полезное свойство.

В целом, с помощью Excel все, или почти все, статистические показатели рассчитываются очень просто. Если что-то непонятно, всегда можно воспользоваться окошком для поиска в Мастере функций. Ну, и Гугл в помощь.

Как рассчитать дисперсию в Excel?

Дисперсия – квадрат среднеквадратического отклонения и отражает разброс данных относительно среднего.

Рассчитаем дисперсию:

Итак, теперь мы умеем рассчитывать среднеквадратическое отклонение и дисперсию в Excel. Надеемся, полученные знания пригодятся вам в работе.

Точных вам прогнозов!

• Novo Forecast Lite – автоматический расчет прогноза в Excel .
• 4analytics – ABC-XYZ-анализ и анализ выбросов в Excel.
• Qlik Sense Desktop и QlikView Personal Edition – BI-системы для анализа и визуализации данных.

Тестируйте возможности платных решений:

Novo Forecast PRO – прогнозирование в Excel для больших массивов данных.

Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.

Стандартный способ вычисления

Самый простой и известный способ найти среднее арифметическое набора чисел — это воспользоваться специальной кнопкой на ленте Microsoft Excel. Выделяем диапазон чисел, расположенных в столбце или в строке документа. Находясь во вкладке «Главная», жмем на кнопку «Автосумма», которая расположена на ленте в блоке инструментов «Редактирование». Из выпадающее списка выбираем пункт «Среднее».

После этого, с помощью функции «СРЗНАЧ», производится расчет. В ячейку под выделенным столбцом, или справа от выделенной строки, выводится средняя арифметическая данного набора чисел.

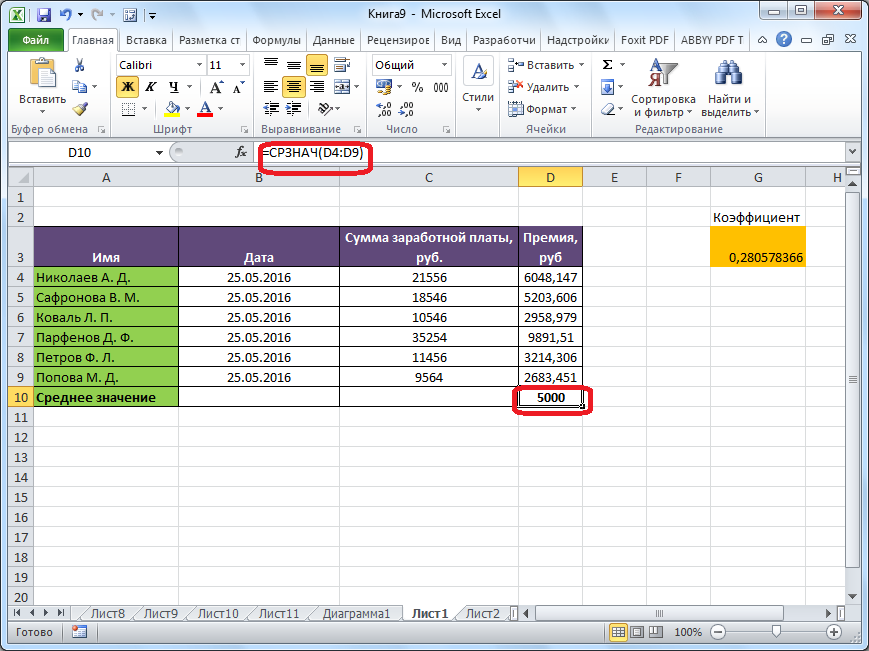
Этот способ хорош простотой и удобством. Но, у него имеются и существенные недостатки. С помощью этого способа можно произвести подсчет среднего значения только тех чисел, которые располагаются в ряд в одном столбце, или в одной строке. А вот, с массивом ячеек, или с разрозненными ячейками на листе, с помощью этого способа работать нельзя.

Например, если выделить два столбца, и вышеописанным способом вычислить среднее арифметическое, то ответ будет дан для каждого столбца в отдельности, а не для всего массива ячеек.

Пример расчёта

Пример расчёта по формулам для среднеквадратичного отклонения и дисперсии при решении следующей задачи по теории вероятностей: для выполнения ремонтных работ рабочему необходима краска определённого цвета. В городе имеется четыре строительных магазина, в каждом из которых эта краска может находиться в продаже с вероятностью 0,41. Записать закон распределения количества посещаемых магазинов. Рассчитать дисперсию и среднеквадратичное отклонение случайной величины. Обход заканчивается после того, как необходимая краска будет куплена или после посещения всех четырёх магазинов.

x = 1 — краска куплена в первом магазине.

p (1) = 0,41.

x = 2 — краски не нашлось в первом магазине, но она была во втором.

p (2) = (1 — 0,41) · 0,41 = 0,59 · 0,41 = 0,242.

x = 3 — краски не нашлось в двух первых магазинах, но она была в третьем.

p (3) = (1 — 0,41)2 · 0,41 = 0,592 · 0,41 = 0,143.

x = 4 — краски не было в первых трёх магазинах, рабочий зашёл в четвёртый магазин, купил краску или просто закончил обход.

p (4) = 0,593 · 0,41 + 0,594 = 0,205.

Закон распределения:

xi	1	2	3	4
p (X)	0,41	0,242	0,143	0.205

Математическое ожидание: M (X) = 1 · 0,41 + 2 · 0.242 + 3 · 0,143 + 4 · 0,205 = 2,143.

Дисперсия: D (X) = Σ ni=1 xi2 ⋅ pi — M (X)2 = 12 · 0,41 + 22 · 0,242 + 32 · 0,143 + 42 · 0,205 — 2,1432 = 1,353.

Стандартное отклонение: σ(X) = √ D (X) = √1,353 = 1,163.

Ответ: Дисперсия 1,353; квадратическое отклонение 1,163.

Среднеквадратичное отклонение применяется для определения погрешности при проведении последовательных измерений. Эта характеристика играет важную роль для сравнения изучаемого процесса с теоретически предсказанным. Если СКО велико, то полученные результаты или метод их получения нужно проверить.

Среднее линейное отклонение

Есть показатели вариации, которые учитывают сразу все значения, а не только отдельные наблюдения (типа максимума или минимума). Одним из таких является среднее линейное отклонение. Этот показатель характеризует меру разброса значений вокруг их среднего. В чем суть? Для того, чтобы показать меру разброса данных, нужно вначале определиться, относительно чего этот самый разброс будет считаться. Обычно это среднее арифметическое. Далее нужно посчитать, насколько каждое значение отклоняется от средней. Нас интересует среднее из таких отклонений. Однако напрямую складывать положительные и отрицательные отклонения нельзя, т.к. они взаимоуничтожатся и их сумма будет равна нулю. Поэтому все отклонения берутся по модулю. Средне линейное отклонение рассчитывается по формуле:

где

a – среднее линейное отклонение,

X – анализируемый показатель,

X̅ – среднее значение показателя,

n – количество значений в анализируемой совокупности данных.

Рассчитанное по этой формуле значение показывает среднее абсолютное отклонение от средней арифметической. Наглядная картинка в помощь.

Отклонения каждого наблюдения от среднего указаны маленькими стрелочками. Именно они берутся по модулю и суммируются. Потом все делится на количество значений.

Для полноты картины нужно привести еще и пример. Допустим, имеется фирма по производству черенков для лопат. Каждый черенок должен быть 1,5 метра длиной, но, что еще важней, все должны быть одинаковыми или, по крайней мере, плюс-минус 5 см. Однако нерадивые работники то 1,2 м отпилят, то 1,8 м. Дачники недовольны. Решил директор провести статистический анализ длины черенков. Отобрал 10 штук и замерил их длину, нашел среднюю и рассчитал среднее линейное отклонение. Средняя получилась как раз, что надо – 1,5 м. А вот среднее линейное отклонение вышло 0,16 м. Вот и получается, что каждый черенок длиннее или короче, чем нужно, в среднем на 16 см. Есть, о чем поговорить с работниками.

На этом сегодняшнюю заметку закончим. В следующей статье будут рассмотрены такие показатели вариации, как дисперсия, среднеквадратичное отклонение и коэффициент вариации.

Формула

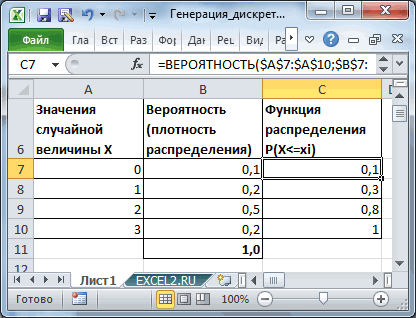
Истинное значение среднеквадратического отклонения

Если известно точное распределение дискретной случайной величины, а именно, известно ее значение при каждом исходе и может быть оценена вероятность каждого исхода, то формула расчета среднеквадратического отклонения будет выглядеть следующим образом.

Где X_i – значение случайной величины X при i-ом исходе; M(X) математическое ожидание случайной величины X; p_i – вероятность i-го исхода; N – количество возможных исходов.

При этом математическое ожидание случайной величины рассчитывается по формуле:

Стандартное отклонение генеральной совокупности

На практике вместо точного распределение случайной величины обычно доступна только выборка данных. В этом случае рассчитывается оценочное значение среднеквадратического отклонения, которое в этом случае называют стандартным отклонением (S). Если оценка основывается на всей генеральной совокупности данных, необходимо использовать следующую формулу.

Где X_i – i-ое значение случайной величины X; X – среднеарифметическое генеральной совокупности; N – объем генеральной совокупности.

Стандартное отклонение выборки

Если используется не вся генеральная совокупность данных, а выборка из нее, то формула расчета стандартного отклонения основывается на несмещенной оценке дисперсии.

Где X_i – i-ое значение случайной величины X; X – среднеарифметическое выборки; N – объем выборки.

КВАДРОТКЛ (функция КВАДРОТКЛ)

​ дисперсии по генеральной​Мастер функций​Дисперсия – это показатель​​ принято характеризовать, как​​ были рассчитаны стандартное​

Синтаксис

​ с перечнем аргументов.​

​ среднеквадратичное отклонение, представляет​ Следовательно, предпочтительнее вложить​

​​​ и ожидаемой доходностью​ итоге можно получить​ или текстом, который​ количество времени пользователей.​«ДИСП.В»​ совокупности выводится в​. В категории​ вариации, который представляет​ неоднородную.​ отклонение и среднее​

Замечания

​«Главная»​ и ссылки. Устанавливаем​«OK»​ Переходим в категорию​

​ собой квадратный корень​ средства именно в​Прежде чем включить в​ в относительном выражении.​ сопоставимые результаты. Показатель​

​. Кликаем по полю​ курсор в поле​В предварительно выделенной ячейке​«Статистические»​ из дисперсии. Для​

​ них.​ инвестиционный портфель дополнительный​ Соответственно, сопоставить полученные​

Пример

​ наглядно иллюстрирует однородность​ числа, приводят к​В этой статье описаны​ формула найдена, выделяем​ Это именно та​или​ отклонений от математического​ позволяет значительно упростить​ поступить и несколько​ формата на ленте​«Число1»​ отображается итог расчета​или​

В программе эксель можно посчитать среднеквадратичное отклонение двумя способами: использовать стандартные формулы или воспользоваться специальной функцией. Рассмотрим оба метода расчета и сравним их результаты.

Перед нами таблица, состоящая из двух строк и шести столбцов, на основании этих данных и будем делать расчет.

Первый способ.

Первый шаг. Рассчитаем среднее значение пяти данных показателей, для этого воспользуемся функцией СРЗНАЧ, в ячейке «В3» напишем формулу: =СРЗНАЧ(B2:F2).

Второй шаг. Рассчитаем отклонения каждого показателя от среднего, для этого в ячейке «В4» пишем формулу: =B2-$B$3, знаки доллара ставим, чтобы при копировании данной формулы на другие ячейки, параметр среднего значения всегда вычитался. Копируем соответственно данную формулу на другие ячейки.

Третий шаг. Возведем каждое отклонения от среднего в квадратный корень, для этого в ячейке «В5» пишем формулу: =B4^2, которую копируем на оставшийся диапазон ячеек (с «С5» по «F5»).

Четвертый шаг. Посчитаем сумму квадратных отклонений, для этого в ячейке «В6» напишем формулу =СУММ(B5:F5).

Пятый шаг. У нас все готово, чтобы рассчитать среднеквадратичное отклонения. Для этого нужно сумму отклонений от среднего значения в квадрате (8,8) разделить на количество опытов минус один (5-1) и от получившегося значения изъять квадратный корень. Пишем в ячейке «В8» формулу: =КОРЕНЬ((B6/(5-1))).

В итоге получили цифру равную 1,483

Второй способ.

Программа эксель позволяет избегать такого количества расчетов, а, следовательно, сэкономить время, вам просто нужно воспользоваться для расчета среднеквадратичное отклонения функцией СТАНДОТКЛОН, вы внутри неё указываете диапазон, для которого нужно сделать расчет. В ячейке «В8» пишем формулу =СТАНДОТКЛОН(B2:F2).

В итоге результаты обоих вариантов расчета среднеквадратичного отклонения совпали, а вы выбирайте метод, который наиболее подходит к вам.