Python numpy array tutorial

1.4.1.1. What are NumPy and NumPy arrays?¶

NumPy arrays

Python objects:	high-level number objects: integers, floating point containers: lists (costless insertion and append), dictionaries (fast lookup)
NumPy provides:	extension package to Python for multi-dimensional arrays closer to hardware (efficiency) designed for scientific computation (convenience) Also known as array oriented computing

>>> import numpy as np
>>> a = np.array()
>>> a
array()

Tip

For example, An array containing:

• values of an experiment/simulation at discrete time steps
• signal recorded by a measurement device, e.g. sound wave
• pixels of an image, grey-level or colour
• 3-D data measured at different X-Y-Z positions, e.g. MRI scan
• …

Why it is useful: Memory-efficient container that provides fast numerical
operations.

In : L = range(1000)

In : %timeit i**2 for i in L
1000 loops, best of 3: 403 us per loop

In : a = np.arange(1000)

In : %timeit a**2
100000 loops, best of 3: 12.7 us per loop

NumPy Reference documentation

• On the web: https://numpy.org/doc/

• Interactive help:

  In : np.array?
  String Form:<built-in function array>
  Docstring:
  array(object, dtype=None, copy=True, order=None, subok=False, ndmin=0, ...
  

• Looking for something:

  >>> np.lookfor('create array') 
  Search results for 'create array'
  ---------------------------------
  numpy.array
      Create an array.
  numpy.memmap
      Create a memory-map to an array stored in a *binary* file on disk.
  

  In : np.con*?
  np.concatenate
  np.conj
  np.conjugate
  np.convolve
  

Синтаксис

Эта функция принимает массив типа numpy (например, массив целых и логических значений NumPy).

Он возвращает новый массив numpy после фильтрации на основе условия, который представляет собой массив логических значений, подобный numpy.

Например, условие может принимать значение массива (]), который является логическим массивом типа numpy. (По умолчанию NumPy поддерживает только числовые значения, но мы также можем преобразовать их в bool).

Например, если условием является массив (]), а наш массив – a = ndarray (]), при применении условия к массиву (a ), мы получим массив ndarray (`1 2`).

import numpy as np

a = np.arange(10)
print(a) # Will only capture elements <= 2 and ignore others

Вывод:

array()

ПРИМЕЧАНИЕ. То же условие условия также может быть представлено как <= 2. Это рекомендуемый формат для массива условий, так как записывать его как логический массив очень утомительно.

Но что, если мы хотим сохранить размерность результата и не потерять элементы из нашего исходного массива? Для этого мы можем использовать numpy.where().

numpy.where(condition )

У нас есть еще два параметра x и y. Что это? По сути, это означает, что если условие выполняется для некоторого элемента в нашем массиве, новый массив будет выбирать элементы из x.

В противном случае, если это false, будут взяты элементы из y.

При этом наш окончательный выходной массив будет массивом с элементами из x, если условие = True, и элементами из y, если условие = False.

Обратите внимание, что хотя x и y необязательны, если вы указываете x, вы также ДОЛЖНЫ указать y. Это потому, что в этом случае форма выходного массива должна быть такой же, как и входной массив

ПРИМЕЧАНИЕ. Та же логика применима как для одномерных, так и для многомерных массивов. В обоих случаях мы выполняем фильтрацию по условию. Также помните, что формы x, y и условия передаются вместе.

Теперь давайте рассмотрим несколько примеров, чтобы правильно понять эту функцию.

Ось Numpy в Python для Sum

Когда мы используем функцию numpy sum() для 2-d массива с параметром axis, она сворачивает 2-d массив до 1-d массива. Он сворачивает данные и уменьшает количество измерений. Но какая ось свернется, чтобы вернуть сумму, зависит от того, установим ли мы ось в 0 или 1. Давайте рассмотрим следующие примеры для лучшего понимания.

Numpy sum с осью 0

import numpy as np

#creating Numpy Array.arange(0, 6).reshape()

print(np_array_2d)
.sum(np_array_2d,)
print(a)

Выход:

 ]

array()

Объяснение:

В приведенном выше примере мы создаем массив размера(2,3), то есть две строки и три столбца. Когда ось установлена на 0. Сразу же функция фактически суммирует столбцы. В результате получается новый массив NumPy, содержащий сумму каждого столбца. Как обсуждалось ранее, ось 0-это направление вдоль строк, но выполняет операции по столбцам. Ось, установленная в 0, относится к агрегированию данных. Поэтому мы сворачиваем строки и выполняем операцию суммирования по столбцам. Таким образом, параметр оси функции sum() представляет, какая ось должна быть свернута.

Numpy Sum С Осью 1

import numpy as np

#creating Numpy Array.arange(0, 6).reshape()

print(np_array_2d)
.sum(np_array_2d,)
print(a)

Выход:

array()

Объяснение:

Как мы знаем, ось 1, согласно конвенции оси. Например, это относится к направлению вдоль столбцов, выполняющих операции над строками. Для функции sum (). Параметр axis-это ось, которая должна быть свернута. Отсюда и в приведенном выше примере. Например, ось установлена на 1 в функции sum (), которая сворачивает столбцы и суммирует строки.

Форма матрицы в Python

Lenght matrix (длина матрицы) в Python определяет форму. Длину матрицы проверяют методом shape().

Массив с 2-мя либо 3-мя элементами будет иметь форму (2, 2, 3). И это состояние изменится, когда в shape() будут указаны аргументы: первый — число подмассивов, второй — размерность каждого подмассива.

Те же задачи и ту же операцию выполнит reshape(). Здесь lenght и другие параметры matrix определяются числом столбцов и строк.

Есть методы и для манипуляции формой. Допустим, при манипуляциях с двумерными или многомерными массивами можно сделать одномерный путём выстраивания внутренних значений последовательно по возрастанию. А чтобы поменять в матрице строки и столбцы местами, применяют transpose().

Параметры

• arr: . Это входной массив, содержащий числа, кумулятивная сумма которых желательна. Если arr не является массивом, выполняется преобразование.
• axis: Это целочисленное значение, которое является необязательным входом. Это ось, по которой вычисляется кумулятивная сумма. По умолчанию именно None вычисляет сумму сплющенного массива.
• Тип: Это необязательный вход. Это тип возвращаемого массива и накопителя, в котором суммируются элементы. Если мы не указываем dtype, то по умолчанию используется dtype a, если только a не имеет целочисленного dtype с точностью меньшей, чем у целого числа платформы по умолчанию. В этом случае используется целое число платформы по умолчанию.

• out: Это и массив, и необязательный вход. Это место, где мы храним результат.

  • Если мы его предоставляем, то он должен иметь форму, на которую транслируются входные сигналы.
  • Если мы его не предоставляем, то возвращается только что выделенный массив.

Строки и столбцы для массива Numpy

ПРИМЕР:

From numpy import asarray
data = , ]
# convert to a numpy array(data)

# step through rows
for row in range(data.shape):
	print(data)

#step through columns
for col in range(data.shape):
	print(data)

ВЫХОД:

ОБЪЯСНЕНИЕ:

В приведенном выше примере мы перечисляем данные каждой строки и столбца. Другими словами, мы достигаем этого, получая доступ к ним через их индекс. Данные дают значение в первой строке и первом столбце. Кроме того, data дает значения в первой строке и во всех столбцах, например, полную первую строку в нашей матрице. Аналогично, data обращается ко всем строкам первого столбца. Прежде всего, при печати строк массива ось Numpy устанавливается в 0, то есть data.shape. Аналогично, ось Numpy устанавливается в 1 при перечислении столбцов.

1.4.1.7. Fancy indexing¶

Tip

NumPy arrays can be indexed with slices, but also with boolean or
integer arrays (masks). This method is called fancy indexing.
It creates copies not views.

Using boolean masks

>>> np.random.seed(3)
>>> a = np.random.randint(, 21, 15)
>>> a
array()
>>> (a % 3 == )
array()
>>> mask = (a % 3 == )
>>> extract_from_a = amask # or,  a
>>> extract_from_a           # extract a sub-array with the mask
array()

Indexing with a mask can be very useful to assign a new value to a sub-array:

>>> aa % 3 ==  = -1
>>> a
array()

Indexing with an array of integers

>>> a = np.arange(, 100, 10)
>>> a
array()

Indexing can be done with an array of integers, where the same index is repeated
several time:

>>> a]  # note:  is a Python list
array()

New values can be assigned with this kind of indexing:

>>> a] = -100
>>> a
array()

Tip

When a new array is created by indexing with an array of integers, the
new array has the same shape as the array of integers:

>>> a = np.arange(10)
>>> idx = np.array(, 9, 7]])
>>> idx.shape
(2, 2)
>>> aidx
array(,
       ])

The image below illustrates various fancy indexing applications

Exercise: Fancy indexing

• Again, reproduce the fancy indexing shown in the diagram above.
• Use fancy indexing on the left and array creation on the right to assign
  values into an array, for instance by setting parts of the array in
  the diagram above to zero.

Пример функции Numpy cumsum ()?

Здесь мы обсудим, как мы можем написать функцию cumsum() из библиотеки numpy.

1. Принимая в качестве входных данных только переменную

В этом примере мы импортируем библиотеку numpy в python. Мы не будем принимать входные данные в виде массива. Мы возьмем целочисленную переменную, а затем применим функцию numpy cumsum () . Следовательно, мы увидим, что преобразование сделано. Давайте рассмотрим этот пример для более детального понимания концепции.

#taking input as a variable
#importing numpy library
import numpy as np

a = 15
print("input taken : ",a)
output = np.cumsum(a)
print("conversion done : ",output)

Выход:

input taken :  15
conversion done :  

Объяснение:

• Во-первых, мы будем импортировать библиотеку numpy с псевдонимом np.
• Затем мы возьмем переменную a, в которой хранится целочисленное значение 15.
• После этого мы напечатаем входное значение.
• Затем мы применим функцию numpy cumsum() и сохраним выходные данные в выходной переменной.
• Наконец, мы напечатаем результат.
• Следовательно, вы можете видеть результат как выполненное преобразование, так как это было единственное целочисленное значение.

2. Принятие входных данных в виде массива

В этом примере мы импортируем модуль numpy. Затем мы будем принимать входные данные в виде массива, а затем применять функцию numpy cumsum () . Наконец, мы увидим совокупную сумму массива. Давайте рассмотрим этот пример для более детального понимания концепции.

#taking input as an array
#importing numpy library
import numpy as np

arr = np.array(, ])
print("input taken : ",arr)
output = np.cumsum(arr)
print("Cumulative sum of array : ",output)

Выход:

input taken :  
 ]
Cumulative sum of array :  

Объяснение:

• Во-первых, мы будем импортировать библиотеку numpy с псевдонимом np.
• Затем мы будем принимать входные данные в виде массива, внутри которого есть несколько целочисленных значений.
• После этого мы напечатаем входной массив.
• Затем мы применим функцию numpy cumsum() и сохраним выходные данные в выходной переменной.
• Наконец, мы напечатаем результат.
• Следовательно, вы можете видеть результат как совокупную сумму массива.

3. Взятие массива и оси в качестве параметра

В этом примере мы импортируем модуль numpy. Затем мы будем принимать входные данные в виде массива и применять ось как 0 и 1 в качестве параметра . Наконец, мы увидим выход на обеих осях и увидим разницу. Давайте рассмотрим этот пример для более детального понимания концепции.

#taking input as an array and axis parameter
#importing numpy library
import numpy as np

arr = np.array(, ])
print("input taken : ",arr)
output = np.cumsum(arr, axis = 0)
print("Cumulative sum of array at axis = 0: ",output)
out = np.cumsum(arr, axis = 1)
print("Cumulative sum of array at axis = 1 : ",out)

Выход:

input taken :  
 ]
Cumulative sum of array at axis = 0:  
 ]
Cumulative sum of array at axis = 1 :  
 ]

Объяснение:

• Во-первых, мы будем импортировать библиотеку numpy с именем as np.
• Затем мы будем принимать входные данные в виде массива, внутри которого есть несколько целочисленных значений.
• После этого мы напечатаем входной массив.
• Затем мы применим функцию numpy cumsum() с массивом, а ось будет равна 0 и 1 и сохранит выходные данные в переменной output и out.
• Наконец, мы напечатаем оба вывода.
• Следовательно, вы можете видеть результат как совокупную сумму массива с и.

4. Взятие массива и типа d в качестве параметра

В этом примере мы импортируем модуль numpy. Тогда мы будем принимать входные данные как массив и как тип данных массива. Наконец-то мы увидим результат. Давайте рассмотрим этот пример для более детального понимания концепции.

#taking input as an array and dtype as a parameter
#importing numpy library
import numpy as np

arr = np.array(, ])
print("input taken : ",arr)
output = np.cumsum(arr, dtype = float)
print("Cumulative sum of array : ",output)

Выход:

input taken :  
 ]
Cumulative sum of array :  

Объяснение:

• Во-первых, мы будем импортировать библиотеку numpy с псевдонимом np.
• Затем мы будем принимать входные данные в виде массива, внутри которого есть несколько целочисленных значений.
• После этого мы напечатаем входной массив.
• Затем мы применим функцию numpy cumsum() с массивом и в качестве параметра и сохраним выходные данные в выходной переменной.
• Наконец, мы напечатаем результат.
• Следовательно, вы можете видеть выходные данные как совокупную сумму массива в типе данных float.

Append NumPy array to another

You can append a NumPy array to another NumPy array by using the append() method.

Consider the following example:

import numpy

a = numpy.array()

b = numpy.array()

newArray = numpy.append(a, b)

print("The new array = ", newArray)

The output will be as follows:

In this example, a NumPy array “a” is created and then another array called “b” is created. Then we used the append() method and passed the two arrays. As the array “b” is passed as the second argument, it is added at the end of the array “a”.

As we saw, working with NumPy arrays is very simple. NumPy arrays are very essential when working with most machine learning libraries. So, we can say that NumPy is the gate to artificial intelligence.

Different methods of normalization of NumPy array

1. Normalizing using NumPy Sum

In this method, we use the NumPy ndarray sum to calculate the sum of each individual row of the array. After which we divide the elements if array by sum. Let us see this through an example.

import numpy as ppool
a=ppool.array(,
                ],dtype="float")
print(a)
b=ppool.ndarray.sum(a,axis=1)
print(b)
c=a/b
print(c)

Output:

This is another you can use for normalizing the array. This method is really effective for row-wise normalization.

2. Normalization using sklearn

Sklearn is a module of python used highly for data science and mining. Using this method also we can normalize the array. It follows a really simple procedure and let us understand it using an example.

from sklearn import preprocessing
print(preprocessing.normalize(, ]))

Output:

3. Normalization using list comprehension

You can also normalize a list in python. List comprehension, in general, offers a shorter syntax, which helps in creating the new list from the existing list. Let us look at it through an example.

list = ]
norm_list = [i / sum(j) for j in list for i in j]
print(norm_list)

Look how we were able to normalize our existing list. Here we can see that we have divided each element in the list by the sum of all elements. This also a good option for normalizing.

4. Normalization using For loop

We also carry forward the normalization process using for loop. Using for loop, we can calculate the sum of all elements. Then divide each element by that sum. Here I advise you to use the NumPy array. While carrying on the division, you may get the error as “list/int” not a suitable data-type.

import numpy as ppool
def _sum(arr):  
      
    sum=0
      
    for i in arr: 
        sum = sum + i 
          
    return(sum)  
  
arr = ppool.array( ) 
n = len(arr)  
ans = _sum(arr)  
print (ans) 
b= arr/ans
print(b)

Output:

Обратитесь в массив списка в Python

Как мы уже обсуждали Списки и Массивы похожи в Python. Там, где основное различие между ними, в том, что массивы позволяют только элементы одного и того же типа данных, в то время как списки позволяют им быть разными.

Поскольку Python не поддерживает обычные массивы, мы можем использовать списки, чтобы изобразить то же самое и попытаться отменить их. Давайте посмотрим на разные методы, следующие, которые мы можем достичь этой задачи,

1. Использование списка нарезка, чтобы изменить массив в Python

Мы можем изменить массив списка, используя нарезка методы. Таким образом, мы фактически создаем новый список в обратном порядке как у оригинального. Давайте посмотрим, как:

#The original array
arr = 
print("Array is :",arr)

res = arr #reversing using list slicing
print("Resultant new reversed array:",res)

Выход :

Array is : 
Resultant new reversed array: 

2. Использование метода обратного ()

Python также предоставляет встроенный метод Это непосредственно меняет порядок элементов списка прямо на исходном месте.

Примечание : Таким образом, мы меняем порядок фактического списка. Следовательно, исходный порядок потерян.

#The original array
arr = 
print("Before reversal Array is :",arr)

arr.reverse() #reversing using reverse()
print("After reversing Array:",arr)

Выход :

Before reversal Array is : 
After reversing Array: 

3. Использование обратного () метода

У нас еще один метод, Что при прохождении со списком возвращает намерение имеющих только элементы списка в обратном порядке. Если мы используем Метод на этом намечном объекте мы получаем новый список, который содержит наш обратный массив.

#The original array
arr = 
print("Original Array is :",arr)
#reversing using reversed()
result=list(reversed(arr))
print("Resultant new reversed Array:",result)

Выход :

Original Array is : 
Resultant new reversed Array: 

1D Массив NP Axis в Python – Особый случай

Оси numpy работают по-разному для одномерных массивов. Большая часть обсуждения, которое мы провели в этой статье, относится к двумерным массивам с двумя осями- строками и столбцами. Массивы 1D отличаются тем, что они имеют только одну ось. Оси Numpy нумеруются так же, как индексы Python, то есть они начинаются с 0. Поэтому в массиве 1D первой и единственной осью является ось 0. Если мы зададим параметр axis как 1 при работе с 1D массивами. Кроме того, он возвращает ошибку.

import numpy as np

#arrays defined.array().array()

print(np_array_1)
print(np_array_2)
.concatenate(,)
.concatenate(,)


print(a)

print(b)

Выход:

array()

IndexError: axis 1 out of bounds [0, 1)

Объяснение:

Как уже упоминалось выше, 1-мерные массивы имеют только одну ось – ось 0. Функция работает правильно, когда параметр оси установлен в 1. Он печатает “а” как комбинированный 1D-массив из двух входных 1D-массивов. В 1D массивах ось 0 не указывает вдоль строк “вниз”, как это происходит в 2-мерном массиве. Однако, когда параметр axis установлен в 1, он не может напечатать “b”. В заключение он поднял indexerror, заявив, что ось 1 находится за пределами границ для одномерных массивов.

1.4.1.5. Indexing and slicing¶

The items of an array can be accessed and assigned to the same way as
other Python sequences (e.g. lists):

>>> a = np.arange(10)
>>> a
array()
>>> a], a2], a-1
(0, 2, 9)

Warning

Indices begin at 0, like other Python sequences (and C/C++).
In contrast, in Fortran or Matlab, indices begin at 1.

The usual python idiom for reversing a sequence is supported:

>>> a)

For multidimensional arrays, indices are tuples of integers:

>>> a = np.diag(np.arange(3))
>>> a
array(,
       ,
       ])
>>> a1, 1
1
>>> a2, 1 = 10 # third line, second column
>>> a
array(,
       ,
       ])
>>> a1
array()

Note

• In 2D, the first dimension corresponds to rows, the second
  to columns.
• for multidimensional , is interpreted by
  taking all elements in the unspecified dimensions.

Slicing: Arrays, like other Python sequences can also be sliced:

>>> a = np.arange(10)
>>> a
array()
>>> a293 # 
array()

Note that the last index is not included! :

>>> a)

All three slice components are not required: by default, start is 0,
end is the last and step is 1:

>>> a13
array()
>>> a)
>>> a3:]
array()

A small illustrated summary of NumPy indexing and slicing…

You can also combine assignment and slicing:

>>> a = np.arange(10)
>>> a5:] = 10
>>> a
array()
>>> b = np.arange(5)
>>> a5:] = b)

Exercise: Indexing and slicing

• Try the different flavours of slicing, using , and
  : starting from a linspace, try to obtain odd numbers
  counting backwards, and even numbers counting forwards.

• Reproduce the slices in the diagram above. You may
  use the following expression to create the array:

  >>> np.arange(6) + np.arange(, 51, 10),
         ,
         ,
         ,
         ,
         ])
  

Exercise: Array creation

Create the following arrays (with correct data types):

,
 1, 1, 1, 1],
 1, 1, 1, 2],
 1, 6, 1, 1]]

,
 2., , , , ],
 , 3., , , ],
 , , 4., , ],
 , , , 5., ],
 , , , , 6.]]

Par on course: 3 statements for each

Hint: Individual array elements can be accessed similarly to a list,
e.g. or .

Hint: Examine the docstring for .

Арифметические операции с матрицей

Вы можете выполнять арифметические операции, такие как сложение, вычитание, умножение и деление между матрицами. В следующем примере вы можете увидеть несколько примеров арифметических операций.

import numpy


# initialize two array
x = numpy.array(, ], dtype=numpy.float64)
y = numpy.array(, ], dtype=numpy.float64)

print('Print the two matrices')
print('X = \n', x)
print('Y = \n', y)

# Elementwise sum; both produce the array
print('\nElementwise addition of two matrices: ( X + Y of Matlab )')
print('Add using add operator: \n', x + y)
print('Add using add function: \n', numpy.add(x, y))

# Elementwise difference; both produce the array
print('\nElementwise subtraction of two matrices: ( X - Y of Matlab )')
print('Subtract using operator: \n', x - y)
print('Subtract using function: \n', numpy.subtract(x, y))

# Elementwise product; both produce the array
print('\nElementwise Multiplication of two matrices: ( X .* Y of Matlab )')
print('Multiply using operator: \n', x * y)
print('Multiply using function: \n', numpy.multiply(x, y))

# Elementwise division; both produce the array
print('\nElementwise division of two matrices: ( X ./ Y of Matlab )')
print('Division using operator: \n', x / y)
print('Division using function: \n', numpy.divide(x, y))

# Elementwise square root; produces the array
print('\nSquare root each element of X matrix\n', numpy.sqrt(x))

# Matrix Multiplication
print('\nMatrix Multiplication of two matrices: ( X * Y of Matlab )')
print(x.dot(y))

Ниже приведен результат работы вышеуказанной программы матрицы numpy.

Примеры работы с NumPy

Подытожим все вышесказанное. Вот несколько примеров полезных инструментов NumPy, которые могут значительно облегчить процесс написания кода.

Математические формулы NumPy

Необходимость внедрения математических формул, которые будут работать с матрицами и векторами, является главной причиной использования NumPy. Именно поэтому NumPy пользуется большой популярностью среди представителей науки. В качестве примера рассмотрим формулу , которая является центральной для контролируемых моделей машинного обучения, что решают проблемы регрессии:

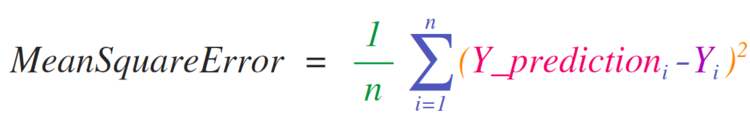
Реализовать данную формулу в NumPy довольно легко:

Главное достоинство NumPy в том, что его не заботит, если и содержат одно или тысячи значение (до тех пор, пока они оба одного размера). Рассмотрим пример, последовательно изучив четыре операции в следующей строке кода:

У обоих векторов и по три значения. Это значит, что в данном случае равно трем. После выполнения указанного выше вычитания мы получим значения, которые будут выглядеть следующим образом:

Затем мы можем возвести значения вектора в квадрат:

Теперь мы вычисляем эти значения:

Таким образом мы получаем значение ошибки некого прогноза и за качество модели.

Представление данных NumPy

Задумайтесь о всех тех типах данных, которыми вам понадобится оперировать, создавая различные модели работы (электронные таблицы, изображения, аудио и так далее). Очень многие типы могут быть представлены как n-мерные массивы:

Необычное индексирование

Необычное индексирование (fancy indexing) — это термин, принятый в
NumPy для описания индексации с использованием целочисленных
массивов.

Предположим, у нас есть массив размера \( 8 \times 4 \)

In : arr = np.empty((8, 4))

In : for i in range(8):
     ...:     arr = i

In : arr
Out: 
array(,
       ,
       ,
       ,
       ,
       ,
       ,
       ])

Чтобы выбрать подмножество строк в определенном порядке, можно
просто передать список или массив целых чисел, указывающих желаемый
порядок:

In : arr]
Out: 
array(,
       ,
       ,
       ])

Использование отрицательных индексов выделяет строки с конца:

In : arr]
Out: 
array(,
       ,
       ])

Передача нескольких индексных массивов делает кое-что другое:
выбирается одномерный массив элементов, соответствующий каждому
кортежу индексов:

In : arr = np.arange(32).reshape((8, 4))

In : arr
Out: 
array(,
       ,
       ,
       ,
       ,
       ,
       ,
       ])

In : arr, ]
Out: array()

Здесь выбраны элементы с индексами , , и
. Независимо от того какая размерность у массива (в нашем
случае двумерный массив), результат такого индексирования — всегда
одномерный массив.

Поведение индексирования в этом случае немного отличается
от того, что могли ожидать некоторые пользователи, а именно:
пользователь мог ожидать прямоугольную область, сформированную путем
выбора поднабора строк и столбцов матрицы. Ниже представлен один из
способов получения таких массивов с помощью необычного индексирования:

In : arr]]
Out: 
array(,
       ,
       ,
       ])

Имейте в виду, что необычное индексирование, в отличие от среза,
всегда копирует данные в новый массив.

Работа с polynomial

В SciPy есть два способа работы с polynomial. Первый использует класс poly1d. Этот класс принимает коэффициенты или корни для инициализации и формирует полиномиальный объект. Когда мы печатаем этот объект, мы видим, что он напечатан, как polynomial. Давайте посмотрим на пример кода:

from numpy import poly1d

# We'll use some functions from numpy remember!!
# Creating a simple polynomial object using coefficients
somePolynomial = poly1d()

# Printing the result
# Notice how easy it is to read the polynomial this way
print(somePolynomial)

# Let's perform some manipulations
print("\nSquaring the polynomial: \n")
print(somePolynomial* somePolynomial)

#How about integration, we just have to call a function
# We just have to pass a constant say 3
print("\nIntegrating the polynomial: \n")
print(somePolynomial.integ(k=3))

#We can also find derivatives in similar way
print("\nFinding derivative of the polynomial: \n")
print(somePolynomial.deriv())

# We can also solve the polynomial for some value, 
# let's try to solve it for 2
print("\nSolving the polynomial for 2: \n")
print(somePolynomial(2))

Другой способ работы с polynomial – использовать массив коэффициентов. Существуют функции, доступные для выполнения операций с polynomial, представленными в виде последовательностей, первый метод выглядит намного проще в использовании и дает вывод в удобочитаемой форме, поэтому я предпочитаю первый для примера.

Дискретное преобразование Фурье (numpy.fft)¶

Прямое преобразование	Обратное преобразование	Описание
fft(a)	ifft(a)	одномерное дискретное преобразование Фурье
fft2(a)	ifft2(a)	двумерное дискретное преобразование Фурье
fftn(a)	ifftn(a)	многомерное дискретное преобразование Фурье
rfft(a)	irfft(a)	одномерное дискретное преобразование Фурье (действительные числа)
rfft2(a)	irfft2(a)	двумерное дискретное преобразование Фурье (действительные числа)
rfftn(a)	irfftn(a)	многомерное дискретное преобразование Фурье (действительные числа)
hfft(a)	ihfft(a)	преобразование Фурье сигнала с Эрмитовым спектром
fftfreq(n)		частоты дискретного преобразования Фурье
fftshift(a)	ifftshift(a)	преобразование Фурье со сдвигом нулевой компоненты в центр спектра

Установка NumPy

Я думаю, вы
прониклись уважением к этому пакету, и пришла пора прикоснуться к «святому
граалю». В начале, как всегда, его нужно установить. Сделать это чрезвычайно
просто, достаточно выполнить в терминале команду:

pip install numpy

Не удивляйтесь,
если этот пакет у вас уже установлен, так как он входит в состав многих других
библиотек. Проверить установку можно командой:

import numpy as np

Если такая
программа выполняется без ошибок, то этот «святой грааль» уже присутствует на
вашем устройстве и готов к истязаниям.

У вас здесь уже
может возникнуть вопрос: почему импорт записан в таком виде? А не просто: import
numpy? Можно и так, но тогда в программе все время придется использовать
префикс numpy. Гораздо удобнее писать две буквы «np». Поэтому
общепринятой практикой стало импортирование этого пакета именно в таком виде. Я
буду следовать сложившейся традиции и делать также.

Параметр дисперсии Numpy

a = Массив, содержащий элементы, дисперсия которых должна быть вычислена

Axis = Значение по умолчанию равно none, что означает вычисление дисперсии 1D-сплющенного массива. Однако ось может быть int или кортежем ints. Если они хотят, чтобы дисперсия вычислялась вдоль какой-либо конкретной оси или осей соответственно. (Необязательно)

dtype = Тип данных, используемый при вычислении дисперсии. По умолчанию используется float64 для массивов целочисленного типа. Для массивов типов float это то же самое, что и массив

out = Альтернативный выходной массив, имеющий тот же размер, что и ожидаемый выходной массив. Но тип бросается, если это необходимо. (Необязательно)

Ddof = Относится к “Дельта-степеням свободы”: делитель, используемый при вычислении, равен N – ddof. Где N – количество элементов. ddof по умолчанию равен нулю. (Необязательно)

Keepdims = , если это значение равно True. Кроме того, уменьшенные оси возвращаются в виде массивов с размером одного измерения. С помощью этой опции результат будет правильно транслироваться по входному массиву. Для значения по умолчанию keepdims не будет передаваться в метод var() подклассов ndarray. Однако любое значение, отличное от значения по умолчанию, действительно проходит. (Необязательно)

1.4.1.2. Creating arrays¶

Manual construction of arrays

• 1-D:

  >>> a = np.array()
  >>> a
  array()
  >>> a.ndim
  1
  >>> a.shape
  (4,)
  >>> len(a)
  4
  

• 2-D, 3-D, …:

  >>> b = np.array(, 3, 4, 5]])    # 2 x 3 array
  >>> b
  array(,
         ])
  >>> b.ndim
  2
  >>> b.shape
  (2, 3)
  >>> len(b)     # returns the size of the first dimension
  2
  
  >>> c = np.array(, 2]], , 4]]])
  >>> c
  array(,
          ],
  
         ,
          ]])
  >>> c.shape
  (2, 2, 1)
  

Exercise: Simple arrays

• Create a simple two dimensional array. First, redo the examples
  from above. And then create your own: how about odd numbers
  counting backwards on the first row, and even numbers on the second?
• Use the functions , on these arrays.
  How do they relate to each other? And to the attribute of
  the arrays?