Калькулятор доходности вкладов

Примеры задач на проценты с решением

Для полного понимания задач на проценты, необходимо решить реальные примеры из жизни. Этим и займемся

Задача 1

Решение:

Всего у магазина 1000 айфонов — это 100%. Отношение 3% к 100 будет равно отношению бракованных айфонов к их общему количеству:

3/100 = Х/ 1000

3 х 1000 = 100 х Х

30 = Х

Ответ: 30 айфонов — бракованные.

Задача 2

Школа купила 250 парт: 225 из них — полностью годны для использования. Какой процент парт исправны, а сколько процентов оказались браком?

Решение:

250 парт — это 100 процентов. По простой пропорции отношения исправных парт к общему числу и их процентов к 100 находим долю.

225/250 = Х/100

225 х 100 = 250 х Х

Х = 90

90 процентов парт — готовы разбежаться по кабинетам, с ними все в порядке. Значит с остальными партами что-то не так: то ли ножки кривые, то ли краска слезла. Выходит: 100 – 90 = 10. 10 процентов парт бракованы.

Ответ: 90% годны и 10% бракованы.

Задача 3

Цена за килограмм арбуза увеличилась на 8 рублей — это на 10% больше прежней цены. Сколько раньше стоил килограмм арбуза?

Решение:

Если 8 рублей — это 10 процентов, то по пропорции находим 100%.

8/Х = 10/100

8 х 100 = 10 х Х

80 = Х

Ответ: до подорожания арбуз стоил 80 рублей за килограмм.

Задача 4

Число собачек-мальчиков в питомнике относится к числу всех собак, как 1/15. Общее число собак в питомнике — 120. Сколько всего собак-мальчиков и каков их процент?

Решение:

Сначала нужно найти число собак-мальчкиков. Нам дано отношение 1/15. По пропорции находим:

1/15 = Х/120

120 = 15 х Х

Х = 8

Число собак-мальчиков — 8. Всего их 120, то есть по еще одной пропорции находим их долю.

8/120 = Х/100

800 = 120 х Х

Х = 6,67%

Ответ: 6.67 процентов собак — мальчики, а всего их 8.

Задача 5

25% фотографий в инстаграме одноклассника — это 150 штук. Сколько всего у него фоток в аккаунте?

Решение:

Если 25% — это 150, то нужно найти значение 100 процентов.

25/100 = 150/Х

0.25 = 150/Х

Х = 600

Ответ: у одноклассника 600 фотографий.

Задача 6

Артем купил 15 яблок — 3 из них оказались гнилыми. Он выбросил их и купил еще 8. Теперь гнилых яблок было 2, а яблок всего 20. Насколько процентов снизилась доля гнилых яблок?

Решение:

Сначала гнилых яблок было 3 из 15 — это 20% от общего количества.

Потом Артем купил еще 8 — теперь их стало 20. Но 2 яблока оказались гнилыми. То есть процент гнилых яблок теперь стал 10%.

20% — 10% = 10%

Ответ: процент гнилых яблок снизился на 10%

Соотношения чисел

Есть случаи, при которых можно использовать простые дроби.

• 10% — десятая часть целого. Чтобы найти десять %, понадобится известное разделить на 10.
• 20% — пятая часть целого. Чтобы вычислить двадцать % от известного, его нужно разделить на 5.
• 25% — четверть целого. Чтобы вычислить двадцать пять %, понадобится известное разделить на 4.
• 50% — половина целого. Чтобы вычислить половину, нужно известное разделить на 2.
• 75% — три четверти целого. Чтобы вычислить семьдесят пять %, нужно известное значение разделить на 4 и умножить на 3.

Задача для тренировки. В черную пятницу вы нашли отличный пиджак со скидкой 25%. В обычный день он стоит 8500 рублей, но сейчас с собой есть только 6400 рублей. Хватит ли средств для покупки?

Как решаем: 100 — 25 = 75, значит нужно заплатить 75% от первоначальной цены. используем правило соотношения чисел: 8500 : 4 * 3 = 6375.

Ответ: средств хватит, так как пиджак стоит 6375 рублей.

Как посчитать разницу в процентах в Excel?

Насколько изменилось значение между двумя величинами в процентах.

Разница в процентах = (новые данные – старые данные) / старые данные * 100%.

В нашем примере закупочная стоимость единицы товара увеличилась на 50%.

Посчитаем разницу в процентах между данными в двух столбцах:

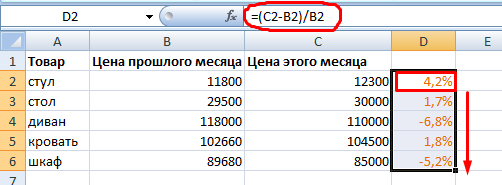
Не забываем выставлять «Процентный» формат ячеек.

Рассчитаем процентное изменение между строками:

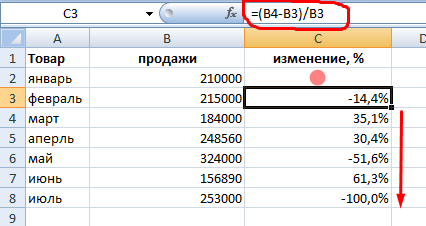
Формула такова: (следующее значение – предыдущее значение) / предыдущее значение.

При таком расположении данных первую строку пропускаем!

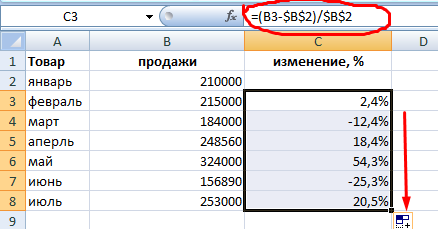
Если нужно сравнить данные за все месяцы с январем, например, используем абсолютную ссылку на ячейку с нужным значением (знак $).

Расчет процентов в Excel

Эксель умеет выполнять многие математические задачи, в том числе и простейший расчет процентов. Пользователю в зависимости от потребностей не составит труда рассчитать процент от числа и число по проценту, в том числе и в табличных вариантах данных. Для этого следует лишь воспользоваться определенными формулами.

Вариант 1: Расчет процентов от числа

Прежде всего давайте выясним, как рассчитать величину доли в процентах одного числа от другого.

Формула вычисления выглядит следующим образом: .
Чтобы продемонстрировать вычисления на практике, узнаем, сколько процентов составляет число 9 от 17

Выделяем ячейку, куда будет выводиться результат и обязательно обращаем внимание, какой формат указан на вкладке «Главная» в группе инструментов «Число». Если формат отличен от процентного, обязательно устанавливаем в поле параметр «Процентный».
После этого записываем следующее выражение: .

Впрочем, так как мы задали процентный формат ячейки, дописывать значение «*100%» не обязательно. Достаточно ограничиться записью «=9/17».

Чтобы посмотреть результат, жмем на клавишу Enter. В итоге получаем 52,94%.

Теперь взглянем, как можно вычислять проценты, работая с табличными данными в ячейках.

1. Допустим, нам требуется посчитать, сколько процентов составляет доля реализации конкретного вида товара от общей суммы, указанной в отдельной ячейке. Для этого в строке с наименованием товара кликаем по пустой ячейке и устанавливаем в ней процентный формат. Ставим знак «=». Далее щелкаем по клеточке с указанием величины реализации конкретного вида товара «/». Потом — по ячейке с общей суммой реализации по всем товарам. Таким образом, в ячейке для вывода результата у нас записана формула.

Чтобы посмотреть значение вычислений, нажимаем Enter.

Мы выяснили определение доли в процентах только для одной строки. Неужели для каждой следующей строки нужно будет вводить подобные вычисления? Совсем не обязательно. Нам надо скопировать данную формулу в другие ячейки. Однако поскольку при этом ссылка на ячейку с общей суммой должна быть постоянной, чтобы не происходило смещение, то в формуле перед координатами ее строки и столбца ставим знак «$». После этого ссылка из относительной превращается в абсолютную.

Наводим курсор в нижний правый угол ячейки, значение которой уже рассчитано, и, зажав кнопку мыши, тянем ее вниз до ячейки, где располагается общая сумма включительно. Как видим, формула копируется и на все другие клетки таблицы. Сразу виден результат подсчетов.

Можно посчитать процентную долю отдельных составляющих таблицы, даже если итоговая сумма не выведена в отдельную ячейку. После форматирования ячейки для вывода результата в процентный формат ставим в ней знак «=». Далее кликаем по ячейке, чью долю надо узнать, ставим знак «/» и набираем сумму, от которой рассчитывается процент. Превращать ссылку в абсолютную в этом случае не нужно.

Затем жмем Enter и путем перетягивания копируем формулу в ячейки, которые расположены ниже.

Вариант 2: Расчет числа по проценту

Теперь посмотрим, как рассчитать число от общей суммы по проценту от нее.

1. Формула для расчета будет иметь следующий вид: . Следовательно, если нам понадобилось посчитать, какое число составляет, например, 7% от 70, то просто вводим в ячейку выражение «=7%*70». Так как в итоге мы получаем число, а не процент, то в этом случае устанавливать процентный формат не надо. Он должен быть или общий, или числовой.

Для просмотра результата нажмите Enter.

Эту модель довольно удобно применять и для работы с таблицами. Например, нам нужно от выручки каждого наименования товара подсчитать сумму величины НДС, которая составляет 18%. Для этого выбираем пустую ячейку в строке с наименованием товара. Она станет одним из составных элементов столбца, в котором будут указаны суммы НДС. Форматируем ее в процентный формат и ставим в ней знак «=». Набираем на клавиатуре число 18% и знак «*». Далее кликаем по ячейке, в которой находится сумма выручки от продажи данного наименования товара. Формула готова. Менять формат ячейки на процентный или делать ссылки абсолютными не следует.

Для просмотра результата вычисления жмем Enter.

Копируем формулу в другие ячейки перетаскиванием вниз. Таблица с данными о сумме НДС готова.

Как видим, программа предоставляет возможность удобно работать с процентными величинами. Пользователь может вычислить как долю от определенного числа в процентах, так и число от общей суммы по проценту. Excel можно использовать для работы с процентами как обычный калькулятор, но также с его помощью легко и автоматизировать работу по вычислению процентов в таблицах.

Опишите, что у вас не получилось.
Наши специалисты постараются ответить максимально быстро.

Механизм работы

До сих пор мы рассматривали работу сложного процента в теории. Рассмотрим, что они из себя представляют на практике, на примере банковских депозитов и инвестиций.

На примере банковского депозита

При выборе банковского депозита вкладчик должен обращать внимание на несколько параметров: надежность банка, его участие в государственной системе страхования, условия пополнения и снятия денег, минимальная сумма на счете. Но главный из них – процентная ставка и условия ее начисления

Механизм сложных процентов подключен к вкладам с капитализацией процентов. А сама ставка, которая будет действовать на вашем счете, называется эффективной. Если вы не планируете снимать начисленный доход в течение всего срока накопления, то логично выбрать вклад именно с капитализацией.

Сравним полученный доход по депозиту с начислением процентов ежегодно, ежеквартально, ежемесячно и ежедневно. Первоначальные условия:

• сумма – 400 000 ₽;
• % ставка – 4 % годовых;
• срок вклада: 1, 2 и 3 года.

Сумма, которую получит вкладчик в конце срока, составит:

Срок депозита	Начисление процентов
1 раз в год	1 раз в квартал	1 раз в месяц	1 раз в день
1 год	416 000	416 241,6	416 296,62	416 323,38
2 года	432 640	433 142,68	433 257,18	433 312,9
3 года	449 945,6	450 730,01	450 908,75	450 995,73

В инвестициях

Сложный процент работает не только в банковской, но и в инвестиционной сфере. Если в банках процесс начисления процентов на проценты называют капитализацией, то в инвестициях – реинвестированием, т. е. повторным инвестированием. Но суть остается одинаковой.

Долгосрочные инвесторы хорошо знакомы с механизмом сложных % и стараются его использовать по максимуму. Рассмотрим, как он работает в различных инвестиционных инструментах.

Облигации

Доходность облигации складывается из двух источников – рост котировок и купоны. Последние выплачиваются в виде % от номинала ценной бумаги. Как правило, раз в полгода.

Эффект сложного процента можно наблюдать на купонных выплатах, но только в одном случае – если вы полученную прибыль не тратите на текущее потребление, а повторно вкладываете в инвестиции, т. е. реинвестируете. Понятно, что на доход от одной облигации мало что можно купить. Но если ценных бумаг несколько десятков или сотен, то сумма достаточна для покупки еще нескольких облигаций.

Полная информация об актуальных стратегиях, которые уже принесли миллионы пассивного дохода инвесторам

Скачать книгу

Например, владелец одной ОФЗ-26212-ПД 2 раза в год будет получать по 35,15 ₽. За год заработает 70,3 ₽. На эти деньги нельзя купить новую ОФЗ. Если облигаций не одна, а, например, 50 штук, то за год доход составит 3 515 ₽. Можно купить еще 3 ОФЗ за 1 085,81 ₽/шт. (котировка на 27.10.2020).

Если вы не держите облигацию до погашения, а пытаетесь заработать на росте котировок, то и в этом случае полученную прибыль от перепродажи лучше реинвестировать для включения механизма сложных %.

Акции

Точно такой же эффект, как описанный в предыдущем примере, может давать реинвестирование дохода от акций в покупку новых акций. Для этого полученные дивиденды не надо выводить со счета, а повторно инвестировать.

Не все эмитенты выплачивают дивиденды. Некоторые инвесторы покупают в свои инвестиционные портфели акции роста, т. е. бумаги, которые в перспективе могут вырасти в цене. Купил дешевле, продал дороже – одна из стратегий инвестирования. Сложный % заработает, если на полученную прибыль от перепродажи увеличится капитал в инвестициях, а не количество вещей в гардеробе.

Аналогично механизм “снежного кома” работает и с другими инструментами инвестиций. Эффект можно усилить, если инвестировать на ИИС, тогда каждый возврат подоходного налога (максимум 52 000 ₽ в год) необходимо опять возвращать на брокерский счет и покупать ценные бумаги.

Как рассчитать сложные проценты

Для того, чтобы просчитать, как приумножить деньги сложными процентами и какую прибыль принесет банковский вклад за несколько лет, нужно знать следующие показатели:

первоначальный размер вклада К0

ставка дохода R

количество лет, за которые нужно просчитать доход n

конечная сумма К

По следующей формуле можно рассчитать эту самую конечную прибыль: К=К0*(1+R)n А просчитав размер конечной суммы, легко можно установить размер прибыли – это разница между конечной и первоначальной суммами. При помощи приведенной выше формулы всегда можно просчитать, какой результат принесет в будущем инвестиция.

     Иногда возникают ситуации, когда нужно, наоборот, вычислить стартовую сумму вклада. Тогда эту формулу нужно преобразовать вот в такой вид: K0=K/(1+R)n С помощью формулы можно узнать и такой параметр, как процентная ставка. Эта информация требуется, когда инвестор, к примеру, хочет узнать, какую ставку ему выбрать, и на какой период нужно сделать вклад, чтобы получить конкретную прибыль. Формула вычисления сложных процентов: R=n?K/K0-1 А вот по этой формуле высчитывается период времени, на который нужно вложить средства, чтобы получить определенную желаемую прибыль: n=log1+R*K/K0

     При расчете срока вклада для получения определенной прибыли следует учитывать тот факт, что практически все банки используют целые периоды. То есть, если расчет по формуле показал, что средства для получения конкретной прибыли нужно вложить на 3 года и 9 месяцев, то нужно понимать, что в реальности необходимо будет положить депозит на 4 полных года. Есть и более сложные примеры расчетов прибыли по сложным процентам. К таким примерам относятся вклады с возможностью пополнения. Допустим, у вкладчика есть депозит, который он ежемесячно пополняет определенной суммой. Как же рассчитать, какую прибыль он получит с такого депозита?

Здесь уже простой формулой расчета не обойтись, нужны более сложные механизмы. Рассмотрим эту задачу на конкретном примере: вкладчик положил на счет 1000$ и каждый месяц добавляет к нему 50$. Допустим, процентная ставка составляет 1% в месяц. Для подсчета конечной суммы через пять лет нужно подставить в приведенные выше формулы показатели за каждый период, т.е. за 60 месяцев. Ведь сумма увеличивается не только за счет процентов, но и за счет ежемесячного добавления. При данных условиях по итогам первого месяца сумма на счету составила 1010$. К ней добавились еще 50$. То есть, для расчета конечной суммы во второй месяц процент нужно начислять уже на 1060$. И так далее, до окончания задуманного срока.

Конечно, каждый раз производить такие вычисления довольно сложно, особенно тем, кто не владеет достаточными познаниями в математике. Да и таблицы такие каждый раз не насоставляешься. Поэтому специально для вычисления сложных процентов по вкладам можно разработать свой калькулятор например в таблице excel.

Итак, очевидна разница между простыми и сложными процентами. Однако, следует отметить, что и схема простых процентов при грамотном ее использовании также может принести довольно хорошие результаты в виде прибыли. Более того, простые проценты являются единственным приемлемым вариантом, когда вкладчик нуждается в регулярном выводе средств со счета. Тогда он просто выводит сумму прибыли, накопившейся за месяц, полгода или год. Тогда как сложные проценты более приемлемы в случае долгосрочного вклада и повторного реинвестирования.

В каких случаях используется начисление простых и сложных процентов?

Формула простых процентов по вкладам применяется, когда полученные проценты плюсуются к телу депозита лишь в конце периода или совсем не прибавляются, а переводятся на другой счет. Формулу сложных процентов используют, когда проценты насчитываются через равные временные промежутки (месяц, квартал, год). Это означает проведение капитализации процентов (когда проценты насчитываются на проценты).

Простые проценты используются в случаях оформления краткосрочных вкладов, период действия которых, в основном, меньше года. Метод сложных процентов применяется при долгосрочных вкладах, которые открываются на срок больше года.

Умножаем на проценты в Excel

Проводя различные вычисления может потребоваться умножить число на определённый процент от него самого или на процент от какого-то другого числа. Часто это может требоваться, чтобы сделать надбавку к цене товара, например, указать цену с учётом фиксированного налога на добавочную стоимость для конкретной категории товаров. К счастью, современный Excel позволяет минимизировать «возню» с формулами и не требует досконально вспоминать уроки математики старших классов.

Большая часть таких операций выполняется в автоматическом режиме и не требует использование специализированных формул. Очень лёгкая в выполнении. Подробно рассмотрим, как это сделать ниже. Инструкция будет актуальна для версий Excel 2007 года и выше.

Ключевые различия между простым интересом и сложным интересом

Ниже приведены основные различия между простым и сложным интересом:

1. Проценты, начисляемые на основную сумму за весь срок кредита, известны как простые проценты. Проценты, начисляемые как на основную сумму, так и на ранее заработанные проценты, называются сложными процентами.
2. Сложный процент дает высокую доходность по сравнению с простым процентом.
3. В Простом Проценте основное значение остается постоянным, в то время как в случае Сложного Процента Основное значение изменяется из-за эффекта сложения.
4. Темпы роста Простых процентов ниже, чем сложных процентов.
5. Расчет простого процента прост, а расчет сложного процента сложен.

пример

Предположим, Алекс депонировал рупий. 1000 в банк под 5% годовых (простой и составной) в год на 3 года. Узнайте общий интерес, который он получит в конце третьего года?

Решение : здесь P = 1000, r = 5% и t = 3 года

Простой интерес =

Сложный процент =

Заключение

Проценты — это плата за использование чужих денег. Существует много причин для выплаты процентов, таких как временная стоимость денег, инфляция, альтернативные издержки и фактор риска. Простой процент быстро рассчитывается, но сложный процент практически сложен. Если вы рассчитываете как простой процент, так и сложный процент для данного принципала, ставки и времени, вы всегда обнаружите, что сложный процент всегда выше, чем простой процент из-за сложного эффекта на него.

Понятие простых процентов и как они рассчитываются

Простые проценты – это проценты, начисляющиеся лишь на первоначальную величину вклада, независимо от количества периодов и их продолжительности. Они считаются один раз по окончанию срока депозита. Это обозначает, что сумма процентов за предыдущий период не учитывается при расчете в следующем. 

Метод расчета простых процентов основан на принципе наращения денег по арифметической прогрессии. Допустим, инвестор в начале года положил в банк депозит на сумму 100 000 руб. под 10% годовых:

• через год он получит сумму, равную первоначально внесенным деньгам плюс начисленные проценты: 100 000 + 10 000 (чтобы высчитать процент нужно сумму вклада умножить на ставку и разделить на 100) = 110 000 (руб.);
• через 2 года сумма составит: 100 000 + (10 000 х 2) = 120 000 (руб.);
• через N лет вкладчик получит: 100 000 + (10 000 х N).

Поскольку банки указывают ставку за год, то чтобы определить доход за другой период (к примеру, 3 месяца), применяя простую ставку процентов, формула будет такой:

S = (P x I x Т / K) / 100, где:

S– сумма насчитанных процентов (руб.);

P– начальная сумма вложенных средств;

I– процентная ставка за год;

Т – срок действия вклада в днях;

K– число дней в году.

То есть при вкладе 100 000 руб. на 3 месяца под 10% годовыхвычисление простых процентовбудет выполняться так:

(100 000 х 10 х 92 / 365) / 100 = 2520,55 (руб.).

Получается, что в конце срока вкладчик получит на руки внесенные 100 000 руб. плюс 2520,55 руб. дохода, т.е. 102 520,55 руб.

Это интересно: Обязанности таможенного брокера, кто это такой

Эффективная процентная ставка

Заявленная номинальная
процентная ставка (например по кредиту
или депозиту) далеко не всегда в полной
мере отражает тот реальный уровень
выплат, которые будут в итоге по ней
выполнены. Например, ставка по депозиту
в 10% годовых вовсе не означает того, что
через год с суммы в 100000 рублей вам будут
начислены проценты в размере 10000 рублей.

То же самое можно сказать
и о кредитах. Заявленная ставка по
кредиту в 12% вовсе не означает того, что
в итоге ваша переплата по нему будет
составлять, например 120000 рублей с суммы
займа в 1000000 рублей. В реальности сумма
переплаты будет выше.

Вот для того, чтобы
отразить реальную сумму процентных
платежей (не только для кредитов и
депозитов, но и при оценке различных
инвестиционных проектов) и было введено
понятие эффективной процентной ставки.

Почему реальная сумма
платежей оказывается больше той, которая
вытекает из указанной номинальной
ставки в процентах годовых? Это происходит
из-за влияния сложных процентов, а также
из-за различных сопутствующих платежей
и комиссий.

Так по обычному депозиту
размещённому под 10% годовых, прибыль
через один год может составлять большую
величину, например в том случае, если
вклад будет с ежемесячной капитализацией
процентов**. Смотрите сами (пример для
суммы вклада в 100000 рублей):

Месяц	Сумма вклада (с капитализацией процентов)	Сумма вклада (без капитализации процентов)
1	100833	100833
2	101672	101666
3	102519	102499
4	103373	103332
5	104234	104165
6	105103	104998
7	105978	105831
8	106861	106664
9	107751	107497
10	108649	108330
11	109554	109163
12	110466	110000

Как видите, при ежемесячной
капитализации процентов итоговая
прибыль по вкладу несколько выше и
составляет 10466 рублей против 10000 рублей
по вкладу без капитализации. То есть, в
данном случае можно сказать, что размер
эффективной процентной ставки составляет
10,46%.

Аналогичная ситуация
складывается и по кредитным платежам,
только в данном случае речь идёт уже не
о проценте прибыли, а о проценте убытка.

Важно знать, что реальная переплата по кредиту (соответствующая эффективной процентной ставке) всегда выше той, которую можно рассчитать исходя из процентной ставки предлагаемой банком. Более того, вполне может
сложиться такая ситуация, когда переплата
по кредиту с меньшей процентной ставкой
в итоге окажется выше той, которая была
бы в том случае, если бы взяли кредит по
большей ставке в другом банке

Более того, вполне может
сложиться такая ситуация, когда переплата
по кредиту с меньшей процентной ставкой
в итоге окажется выше той, которая была
бы в том случае, если бы взяли кредит по
большей ставке в другом банке.

Это происходит по
следующим причинам:

1. Банки в полной мере
   используют все преимущества сложного
   процента;
2. Помимо процентов по
   кредиту с заёмщика могут взиматься
   дополнительные комиссии (страховка,
   затраты на обслуживание кредита и
   т.д.).

Следует иметь ввиду,
что по закону банки обязаны сообщать
клиентам реальную сумму переплаты по
кредиту.

** Ежемесячная капитализация
процентов предполагает начисление
процентов на остаток по вкладу каждый
месяц. Например при ставке в 10% годовых,
ежемесячно будет начисляться процент
в 10/12=0,833%.

Вы можете поделиться этой статьёй на своей странице в соцсетях:

Словарь трейдера

olegas ›

Торгую га финансовых рынках с 2008 года. Сначала это был FOREX, затем фондовая биржа. Сначала занимался преимущественно трейдингом (краткосрочными спекуляциями на валютных рынках), но сейчас все больше склоняюсь к долгосрочным инвестициям на фондовом рынке. Хотя иногда, дабы не терять форму и держать себя в тонусе, балуюсь спекуляциями на срочном рынке (фьючерсы, опционы). Пишу статьи на сайт ради удовольствия.