Python set() function

Операции с множествами Python

Множества могут использоваться для выполнения математических операций: объединение, пересечение и симметричная разница.

Рассмотрим следующие два множества:

>>> A = {1, 2, 3, 4, 5}
>>> B = {4, 5, 6, 7, 8}

Объединение множеств

Объединение A и B — это множество всех элементов из обоих множеств.

Объединение  осуществляется с помощью оператора |. Эту же операцию можно осуществить с помощью метода union().

# инициализируем A и B
A = {1, 2, 3, 4, 5}
B = {4, 5, 6, 7, 8}

# используем оператор |
# Вывод: {1, 2, 3, 4, 5, 6, 7, 8}
print(A | B)

Протестируйте следующие примеры:

# используем функцию union
>>> A.union(B)
{1, 2, 3, 4, 5, 6, 7, 8}

# используем функцию union для B
>>> B.union(A)
{1, 2, 3, 4, 5, 6, 7, 8}

Пересечение множеств питон (python)

Пересечение A и B – операция получения набора элементов, которые являются общими для обоих множеств.

Пересечение осуществляется с помощью оператора &. Эту же операцию можно произвести с помощью метода intersection().

# инициализируем A и B
A = {1, 2, 3, 4, 5}
B = {4, 5, 6, 7, 8}

# используем оператор &
# Вывод: {4, 5}
print(A & B) 

Протестируйте следующие примеры:

# используем функцию intersection для A
>>> A.intersection(B)
{4, 5}

# используем функцию intersection для B
>>> B.intersection(A)
{4, 5}

Определение разницы множеств

Разница A и B (A — B) – операция получения множества элементов, которые принадлежат только  A, но не принадлежат B. Точно так же,  B — A представляет собой множество элементов принадлежащих B , но не принадлежащих А.

Разница определяется с помощью оператора -. или метода difference().

# инициализируем A и B
A = {1, 2, 3, 4, 5}
B = {4, 5, 6, 7, 8}

# используем оператор - для A
# Вывод: {1, 2, 3}
print(A - B)

Протестируйте следующие примеры:

# используем функцию difference для A
>>> A.difference(B)
{1, 2, 3}

# используем оператор - для B
>>> B - A
{8, 6, 7}

# используем функцию difference для B
>>> B.difference(A)
{8, 6, 7}

Симметричная разница множеств

Симметричная разница A и B — это множество элементов в A и B, за исключением тех, которые являются общими для обоих множеств. Она определяется с помощью оператора ^ или метода symmetric_difference().

# инициализируем A и B
A = {1, 2, 3, 4, 5}
B = {4, 5, 6, 7, 8}

# используем оператор ^
# Вывод: {1, 2, 3, 6, 7, 8}
print(A ^ B)

Протестируйте следующие примеры:

# используем функцию symmetric_difference для A
>>> A.symmetric_difference(B)
{1, 2, 3, 6, 7, 8}

# используем функцию symmetric_difference для B
>>> B.symmetric_difference(A)
{1, 2, 3, 6, 7, 8}

Operations with elements

You can get the number of elements in the set using the function .

You can also iterate over all the elements of the set (in an undefined order!) using the loop :

None

primes = {2, 3, 5, 7, 11}
for num in primes:
    print(num)

You can check whether an element belongs to a set using the keyword
: expressions like return a value of type .
Similarly there’s the opposite operation .
To add an element to the set there is the method :

None

A = {1, 2, 3}
print(1 in A, 4 not in A)
A.add(4)

There are two methods to remove an element from a set:
and . Their behavior varies
only in case if the deleted item was not in the set.
In this case the method does nothing and the method
throws exception .

Finally, removes one random element from the set and returns its value. If the set is empty, generates
the exception .

You can transform a set to list using the function .

Выбор случайного элемента из последовательности

Пакет random из стандартной библиотеки Python имеет много полезных функций. Но одна выделяется на общем фоне — .

Эта функция позволяет вам выбирать случайный элемент из индексируемой последовательности, например, из списка, кортежа или даже из строки.

import random as r
my_list = 
print(r.choice(my_list))

# Случайный элемент

Применение на практике

Можно создать функцию для выбора книги. Она будет получать последовательность из книг, выбирать одну из них случайным образом, удалять выбранный элемент из списка и возвращать его в виде строки.

# Импортируем только нужную нам функцию
from random import choice

def book_picker(books):
    book_choice = choice(books)
    books.remove(book_choice)    
    return f"You picked {book_choice}"

books = 

print(book_picker(books)) # Случайный выбор

print(books) # Оставшиеся книги

Ограничения и исключения

Если вы попытаетесь использовать для неиндексируемой последовательности, например, для словаря, множества или числовых типов, Python выдаст ошибку.

# Со словарем
import random as r
scores = {"Jhon": 4, "Ben": 3, "Diana": 5}

print(r.choice(my_scores)) # Key error

А если последовательность будет пустой, вы получите .

# С пустой последовательностью
import random as r
empty_list = []

print(r.choice(empty_list)) # Index error

Как удалить элементы из множества?

Это можно сделать с помощью методов discard() и remove(). Различие между ними состоит в том, что при использовании discard(), если элемент не существует во множестве, оно остается неизменным. А метод remove() выдаст ошибку.

Следующий пример иллюстрирует это.

# инициализируем my_set
my_set = {1, 3, 4, 5, 6}
print(my_set)

# удаляем элемент
# Вывод: {1, 3, 5, 6}
my_set.discard(4)
print(my_set)

# удаляем элемент
# Вывод: {1, 3, 5}
my_set.remove(6)
print(my_set)

# удаляем элемент,
# который отсутствует в my_set
# Вывод: {1, 3, 5}
my_set.discard(2)
print(my_set)

# удаляем элемент,
# который отсутствует в my_set
# Если вы раскомментируете строку 27,
# то получите ошибку.
# Вывод: KeyError: 2

#my_set.remove(2) 

Точно так же можно удалить и вернуть элемент, используя метод pop(). Но нет способа определить, какой элемент будет извлечен.

Мы также можем удалить все элементы из множества, используя метод clear().

# инициализируем my_set
# Вывод: множество уникальных элементов
my_set = set("HelloWorld")
print(my_set)

# извлекаем элемент
# Вывод: случайный элемент
print(my_set.pop())

# извлекаем еще один элемент
# Вывод: случайный элемент
my_set.pop()
print(my_set)

# очищаем my_set
#Вывод: set()
my_set.clear()
print(my_set)

Какие бывают сокеты для процессоров

Собственно, смена процессора на более быстрый (с большей частотой), это часть апгрейда компьютера. С процессором, частота которого выше, быстрее работают программы, такая смена может позволить запускать более современные игры (которые, возможно, старый «камень» «не тянул»).

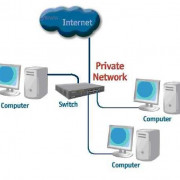
Один из важных критериев подбора нового процессора для апгрейда ПК — подходящий для его установки на материнскую плату сокет. Сокетом называется разъем на материнской плате для установки процессора. Внешне он выглядит как пластиковый квадратный разъем с большим количеством контактов (дырочек под ножки процессора или пружинящих «лапок», которые будут касаться контактов процессора).

На сегодняшний день известно много видов сокетов (как под процессоры Intel, так и AMD), многие из которых уже устарели.

Виды сокетов для процессоров Intel:

Socket 1, 2, 3, 4, 5, 6, 7, 8, Sоcket 370 (это уже для Pentium 3), 423, 478 (для первых Pentium 4, очень многие покупали такие компьютеры), 603/604, PAC418 и 611, LGA771, .LGА775 (еще часто встречается и вполне неплохо работает), 1567, 1366, 1156, 1155, 2011, 1356, 1150, 1151.

Полезный совет: как узнать какой сокет на вашей материнской плате? Если вы знаете сокеты «в лицо», просто раскрутите корпус, снимите кулер процессора и посмотрите. Также можно, не снимая кулера, найти название материнской платы (написано на ней) и найти ее описание в интернете. Если вы с техникой «на вы», лучше найдите документы, в которых описана конфигурация компьютера и прочитайте описание материнской платы там.

Виды сокетов для процессоров AМD:

Super Socket 7, Socket A (462) (процессоры K7 (помните названия Athlon, Athlon, Sempron, Duron?), 754, 939, 940, AM2, AM2+, AM3, AM3+, FМ1 и 2, FМ2+, F, F+, С32, G34.

Сегодня в продаже чаще всего присутствуют процессоры (и, соответственно, материнские платы) с сокетами 2011-2015 годов выпуска. Для Intel это 1150, 1155, 1156. Для AMD это AM2+, AM3+, FM1 и 2.

Обратите внимание, что процессор в сокет должен устанавливаться без особых физических усилий. Если же каким-то чудесным образом процессор установить в неподходящий сокет, он работать не будет

Полезный совет: приобретать ли новую материнскую плату и процессор, если вы увидели в документах, что в вашем компьютере установлена материнка и процессор LGA 775, к примеру? Однозначного ответа я дать не могу. Подумайте сами — если скорость работы компьютера вас устраивает, и вы можете решить все свои задачи, то апгрейд излишен, не тратьте деньги. Если же для запуска необходимых вам программ и игр тратится очень много времени, то, наверное, стоит задуматься об обновлении железа.

Subsets and supersets

If all elements of set A are contained withing set B, A is called a subset of
B and B a superset of A.

python_subset_superset.py

#!/usr/bin/python3

set1 = { 'a', 'b', 'c', 'd', 'e' }
set2 = { 'a', 'b', 'c' }
set3 = {'x', 'y', 'z' }

if (set2.issubset(set1)):
    print("set2 is a subset of set1")
    
if (set1.issuperset(set2)):
    print("set1 is a superset of set2")    
    
if (set2.isdisjoint(set3)):
    print("set2 and set3 have no common elements")     

In the example, we use , ,
and methods.

if (set2.issubset(set1)):
    print("set1 is a subset of set2")

With the method we check if is a subset of .

if (set1.issuperset(set2)):
    print("set1 is a superset of set2")   

With the method we check if is a superset of .

if (set2.isdisjoint(set3)):
    print("set2 and set3 have no common elements")      

With the method we check if and have no
common elements.

$ ./python_subset_superset.py 
set1 is a subset of set2
set1 is a superset of set2
set2 and set3 have no common elements

This is the output.

Что есть в других языках

В языке c++ есть структура , которая поддерживает операции изменения, проверку на наличие, следующий / предыдущий по величине элемент, а также по всем элементам. Но тут нет операций получения элемента по индексу и индекса по значению, так что надо искать дальше (индекс элемента — количество элементов, строго меньших данного)

И решение находится достаточно быстро: из . Эта структура в дополнение к возможностям имеет быстрые операции и , так что эта структура — именно то, что мы ищем.

Она реализована с помощью красно-чёрных деревьев. Смысл этой струкруты в том, что все элементы образуют собой двоичное дерево поиска, которое балансируется так, чтобы высота не превышала логарифм. Нам это даёт возможность с помощью одного спуска по дереву выполнить необходимые операции. Также с этой задачей может справиться Декартово дерево (Дерамида) по неявному ключу или AVL дерево.

Таким образом, целью этой статьи станет поиск аналога этой структуры в Python.

Операции срезов

Срез — это не что иное, как способ обратиться к определенной части последовательности. В Python срезы позволяют нам проделывать различные трюки.

Разворот последовательности

# Разворот списков
lst = 

lst = lst

print(lst) # 

# Разворот строк

string = "Dog running on the park"

string = string

print(string) # krap eht no gninnur goD

Практический пример

Функция, возвращающая последовательность до заданного индекса:

def cutoff(seq, index):
    if not len(seq) > index:
        return "Sorry the index is bigger than the sequence"

    return seq

long_string = "This is a long description of a blog post about Python and technology"

print(cutoff(long_string, 15))
# This is a long 

print(cutoff(long_string, 70))
# Sorry the index is bigger than the sequence

Назначение в Python

Множества (set) в питоне появились не сразу, и здесь они представлены как неупорядоченные коллекции уникальных и неизменяемых объектов. Коллекции, которые не являются ни последовательностями (как списки), ни отображениями (как словари). Хотя с последними у множеств много общего.

Можно сказать, что set напоминает словарь, в котором ключи не имеют соответствующих им значений

Множества:

• Дают возможность быстро удалять дубликаты, поскольку, по определению, могут содержать только уникальные элементы;
• Позволяют, в отличие от других коллекций, выполнять над собой ряд математических операций, таких как объединение, пересечение и разность множеств;

Пример set-ов в Python:

Стилизация print

icecream

Для форматирования вывода существует одна удобная библиотека под названием icecream. Она помогает упростить написание логов или принтов для отладки. Рассмотрим пример её работы:

Чтобы подключить информацию о том, в каком месте программы происходит вывод, необходимо добавить всего лишь один аргумент в конфигурации модуля:

Это помогает более точно понять в каком месте происходит сбой в работе программы:

Также можно поменять префикс, который добавляется в начале строки, по дефолту он задан “ic|”. Удобно добавить время для вывода, чтобы видеть в какой момент времени и сколько занимал переход от одного принта к другому.

Если у вас уже имеются расставленные принты в коде, то легко можно переприсвоить print на ic:

Рассмотрим пример вывода более сложных структур, например, словарей:

Как видно на скриншоте, то вывод данных в таком формате читать гораздо легче, нежели обычный принт.

Также эта библиотека предоставляет возможность стилизовать вывод в зависимости от предоставляемых данных. Например, если есть необходимость дополнительно оформлять текст ошибки (Exception) или есть желание дополнительно выводить тип данных:

colorama

Еще одна полезная библиотека — colorama, она позволит раскрашивать текст в консоли. Её удобно использовать совместно с библиотекой icecream. Рассмотрим пару примеров:

Python set operations

With Python sets we can perform specific operations: union, intersection,
difference, and symmetric difference.

python_set_operations.py

#!/usr/bin/python3

set1 = { 'a', 'b', 'c', 'c', 'd' }
set2 = { 'a', 'b', 'x', 'y', 'z' }

print("Set 1:", set1)
print("Set 2:", set2)
print("intersection:", set1.intersection(set2))
print("union:", set1.union(set2))
print("difference:", set1.difference(set2))
print("symmetric difference:", set1.symmetric_difference(set2))

The example shows four set operations.

print("intersection:", set1.intersection(set2))

The method carries out the intersection operation, which
returns elements that are both in and .

print("union:", set1.union(set2))

The method carries out the union operation,
which returns all elements from both sets.

print("difference:", set1.difference(set2))

The method carries out the difference operation, which returns
elements that are in the but not in .

print("symmetric difference:", set1.symmetric_difference(set2))

The method carries out the symmetric difference
operation, which returns elements that are in or , but not in both.

$ ./python_set_operations.py 
Set 1: {'c', 'b', 'a', 'd'}
Set 2: {'y', 'b', 'a', 'x', 'z'}
intersection: {'b', 'a'}
union: {'b', 'a', 'z', 'c', 'x', 'y', 'd'}
difference: {'c', 'd'}
symmetric difference: {'z', 'c', 'x', 'y', 'd'}

This is a sample output.

It is possible to perform these operations using &, |, -, and ^
operators.

python_set_operations2.py

#!/usr/bin/python3

set1 = { 'a', 'b', 'c', 'c', 'd' }
set2 = { 'a', 'b', 'x', 'y', 'z' }

print("Set 1:", set1)
print("Set 2:", set2)
print("intersection:", set1 & set2)
print("union:", set1 | set2)
print("difference:", set1 - set2)
print("symmetric difference:", set1 ^ set2)

The example shows four set operations using operators.

Bintrees

Так есть же модуль bintrees! Это же то, что нам нужно? И да, и нет. Его разработка была приостановлена в 2020 году со словами .

Пакет предлагает нам несколько структур. К сожалению, ни одна из них не поддерживает операции и подобные, так что эти струкруты являются аналогами . Посмотрим же, на что они способны:

Название говорит само за себя, — красно-чёрное дерево, — несбалансированное двоичное дерево, префикс означает реализацию на (соответственно, необходимо наличие , если используется на Windows).

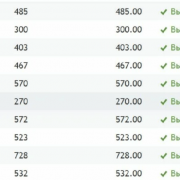
Задача	AVLTree	FastAVLTree	RBTree	FastRBTree	BinaryTree	FastBinaryTree
Добавление	21.946	2.285	20.486	2.373	11.054	2.266
Проверка на наличие	5.86	2.821	6.172	2.802	6.775	3.018
Цикл по всем элементам	0.935	0.297	0.972	0.302	0.985	0.295
Удаление	12.835	1.509	25.803	1.895	7.903	1.588

Результаты тестирования отчётливо показывают нам, почему использовать деревья поиска на Python — плохая идея в плане производительности. А вот в интеграции с всё становится намного лучше.

Оказывается, эта структура и очень похожи по производительности. Все 3 Fast версии структур достаточно близки, поэтому будем считать, что оттуда мы используем .

Задача	SortedSet	FastAVLTree
Добавление	3.924	2.285
Проверка на наличие	1.198	2.821
Цикл по всем элементам	0.162	0.297
Получение индексов	3.959	n/a
Получение значений по индексам	4.909	n/a
Удаление	2.933	1.509

Как мы видим, AVL в полтора раза быстрее в скорости добавления элементов и почти в 2 раза быстрее в операциях удаления. Но он в те же 2 раза медленнее в проверке на наличие и цикле по всем элементам. К тому же не стоит забывать, что 2 операции он выполнять не умеет, то есть не является тем , что мы ищем.

Использование:

Свойства методов и операторов

Как показано выше, данные операции, за некоторым исключением, выполнятся двумя способами: при помощи метода или соответствующего ему оператора (например и оператор ). Главным и основным их различием является то, что метод может принимать в качестве аргумента не только , но и любой итерируемый объект, в то время, как оператор требует в качестве операндов наличие фактических множеств.

Но есть и сходства. Например, важным является то, что некоторые операторы и методы позволяют совершать операции над несколькими сетами сразу:

Тем интереснее, что оператор симметрической разности позволяет использовать несколько наборов, а метод – нет.

Frozen Sets

Python provides another built-in type called a frozenset, which is in all respects exactly like a set, except that a frozenset is immutable. You can perform non-modifying operations on a frozenset:

>>>

But methods that attempt to modify a frozenset fail:

>>>

Frozensets are useful in situations where you want to use a set, but you need an immutable object. For example, you can’t define a set whose elements are also sets, because set elements must be immutable:

>>>

If you really feel compelled to define a set of sets (hey, it could happen), you can do it if the elements are frozensets, because they are immutable:

>>>

Likewise, recall from the previous tutorial on dictionaries that a dictionary key must be immutable. You can’t use the built-in set type as a dictionary key:

>>>

If you find yourself needing to use sets as dictionary keys, you can use frozensets:

Оценка производительности

pympler

Потребление памяти в Python отдельная проблема, которой можно посвятить много времени, поэтому зачастую приходится следить за тем, чтобы python не сожрал всю оперативку. Для проверки памяти есть замечательный модуль pympler, который поможет не только посмотреть память, занимаемую объектом, но также поможет проследить за памятью, которую занимают отдельные классы или типы данных:

Проследим за изменением памяти, занимаемой классом A:

И в целом за памятью, занимаемой различными структурами

py-spy

Но знать распределение памяти зачастую недостаточно, так как программа может тормозить и не выполнять работу за ожидаемое время. В таком случае необходимо отследить, какие процессы сколько времени занимают.

В таком случае можно воспользоваться библиотекой py-spy, она позволяет без остановки программы проверить, сколько времени какие процессы в ней занимают. Установить библиотеку можно через pip install py-spy. Усложним код предыдущей программы, создадим дополнительный модуль sec.py:

модуль main.py:

Теперь через терминал достаточно прописать команду py-spy top — python main.py и вы будете получать информацию о времени работы каждого метода программы:

Вопрос 8. В чём разница между remove, pop и del?

Сложность: (ー_ー)

Каждый из этих трёх методов (точнее, двух методов и одной команды) удаляет элементы списка. Но каждый делает это по-своему и, соответственно, применяется в разных ситуациях.

remove()

Метод remove() удаляет из списка первое совпадающее значение.

Возьмём список и удалим из него элемент ‘b’:

Первая ‘b’ исчезла, но вторая ‘b’ осталась в списке.

pop()

Метод pop() удаляет элемент по индексу и возвращает этот элемент:

Индексация в Python идёт с нуля, поэтому элемент с индексом 2 — третий по счёту. В последних строчках мы вывели изменённый список.

del

Команда del тоже удаляет элемент списка по его индексу, но имеет отличный от pop() синтаксис и ничего не возвращает:

Мы недосчитались четвёртого по индексу (и пятого по счёту) элемента, то есть ‘b’.

Также команда del может удалять из списка срезы (slices):

При указании границ среза в Python последний элемент в срез не входит. Поэтому из списка удалены элементы с третьего (индекс 2) по пятый (индекс 4), исключая последний, то есть 66.25 и 333.

Наконец, del может удалять целые переменные.

Создание объекта

Мы можем создать пустой счетчик или начать с некоторых начальных значений.

from collections import Counter

# empty Counter
counter = Counter()
print(counter)  # Counter()

# Counter with initial values
counter = Counter()
print(counter)  # Counter({'a': 2, 'b': 1})

counter = Counter(a=2, b=3, c=1)
print(counter)  # Counter({'b': 3, 'a': 2, 'c': 1})

Мы также можем использовать любой Iterable в качестве аргумента для создания объекта Counter. Таким образом, строковый литерал и список также могут использоваться для создания объекта Counter.

# Iterable as argument for Counter
counter = Counter('abc')
print(counter)  # Counter({'a': 1, 'b': 1, 'c': 1})

# List as argument to Counter
words_list = 
counter = Counter(words_list)
print(counter)  # Counter({'Dog': 2, 'Cat': 1, 'Horse': 1})

# Dictionary as argument to Counter
word_count_dict = {'Dog': 2, 'Cat': 1, 'Horse': 1}
counter = Counter(word_count_dict)
print(counter)  # Counter({'Dog': 2, 'Cat': 1, 'Horse': 1})

Как я упоминал выше, мы также можем использовать нечисловые данные для значений счетчика, но это нарушит назначение класса Counter.

# Counter works with non-numbers too
special_counter = Counter(name='Pankaj', age=20)
print(special_counter)  # Counter({'name': 'Pankaj', 'age': 20})

Функции листингов

Функции – это, пожалуй, главное преимущество Python над другими языками программирования. К спискам можно применять основные встроенные функции.

Рассмотрим наиболее популярные из них:

list(range( )) – если стоит задача создать последовательный список, то используется функция range. Эта функция имеет следующие формы:

1. range(end). Применяется, когда необходимо создать листинг от нуля до конечного числа.
2. range(start, end). Задается и начальное и конечное число.
3. range(start, end, step). Параметром step задается характеристика выбора. Например, если нужно выбрать каждое пятое число из последовательности от 1 до 21, то полученный листинг будет иметь вид: .

Функция range способна значительно сократить объем кода.

• len(list) – позволяет узнать, сколько элементов в списке.
• sorted(list, ) – сортирует объекты списка по возрастанию.
• max(list) – возвращает наибольший элемент.
• min(list) – противоположная функция – позволяет вернуть элемент с минимальным значением.

Также можно использовать другие встроенные функции:

• list(tuple) – преобразует объект кортежа в список.
• sum(list) – суммирует все элементы в списке, если все значения являются числами, применяется как к целым числам, так и к десятичным дробям. Однако она справляется не всегда корректно. Если в списке есть нечисловой элемент, функция выдаст ошибку: «TypeError: unsupported operand type(s) for +: ‘int’ and ‘str’».

Methods for Sets

add(x) Method: It adds the item x to a set if it is non-preexisting.

A = {"AA", "BB", "CC"}
A.add("VV")

This will add VV in A set.

union(s) Method: It returns a union of two set.Using the operator ‘|’between 2 existing sets is the same as writing My_Set1.union(My_Set2)..

A = {"AA", "BB", "CC"}
B = {"MM", "NN"}
Z = A.union(B)
OR
Z = A|B

Set population set will have components of both A and B.

intersect(s) Method: It returns an intersection of two givensets. The ‘&’ operator can be used in this operation.

S = A.intersection(B)

Set victims will contain the common elements of A and B.

difference(s) Method: Returns a set containing all the elements which are existing in the first set but not present in the second set. We can use ‘-‘ operator here.

W = A.difference(B)
OR
S = A – B

Set safe will have all the elements that are in A but not in B.

clear() Method: The whole existing set will become empty.

B.clear()

Clears B set