Остаток от деления в python 3 и целая часть при делении

Функция sqrt() — квадратный корень

Функция sqrt() вычисляет и возвращает значение квадратного корня из переданного десятичного числа.

Синтаксис:

decimal.Decimal(decimal-number).sqrt()

Пример:

import decimal as d

d.getcontext().prec = 3

val = d.Decimal(122.20)
sqrt = val.sqrt()
print("Decimal Number: ",val)
print("Square root of the decimal number: ",sqrt)

Выход:

Decimal Number:  122.2000000000000028421709430404007434844970703125
Square root of the decimal number:  11.1

Снова обратите внимание, как объявленное значение содержит полное десятичное число, в то время как вычисленное значение соответствует нашему набору точности из 3 цифр

Программа на Python с переменными

Рассмотрим пример иллюстрирующий математическую модель описывающий
траекторию полета мяча в воздухе. Из второго закона Ньютона,
предполагая незначительное сопротивление воздуха, мы можем вывести
зависимость вертикального положения \( y \) мяча от времени
\( t \):
$$
\begin{equation*}
\tag{1}
y = v_0 t -0.5 g t^2
\end{equation*}
$$

где \( v_0 \) — начальная скорость, \( g \) — ускорение
свободного падения, значение которого положим равным \( 9.81 \) м/c \( ^2 \).

Сценарий

Рассмотрим сценарий на Python для вычисления по простой
формуле. Предположим, что сценарий у нас сохранен в виде текста в
файле ball.py

# -*- coding: utf-8 -*-
# Программа для вычисления положения мяча при вертикальном движении

v0 = 5       # Начальная скорость
g = 9.81     # Ускорение свободного падения
t = 0.6      # Время

y = v0*t - 0.5*g*t**2

Разбор сценария

Сценарий на языке Python — это текстовый файл (в нашем случае
ball.py), содержащий некоторые
инструкции. Мы можем читать сценарий и понимать, что программа
способна делать, но сам сценарий не выполняет никаких действий на
компьютере, пока интерпретатор Python не прочитает текст сценария и не
преобразует его в некоторые действия.

Когда сценарий запущен в интерпретаторе Python, он разбирается и выполняется
построчно. Первые две строки

# -*- coding: utf-8 -*-
# Программа для вычисления положения мяча при вертикальном движении

являются

комментариями*, т.е. как только встречается символ ,
интерпретатор Python воспринимает оставшуюся часть строки как
комментарий, пропускает ее и переходит к следующей строки.

Замечание

В первой строке указывается кодировка,
в которой сохранен файл сценария (в нашем случае *— это UTF8). Если в
сценарии не предполагается использование не ASCII символов, то первую
строку можно опустить. Однако, мы можем использовать
кириллический текст, поэтому в наших сценариях мы всегда будем
указывать кодировку.

Следующие 3 строки, интерпретируемые Pyhton:

v0 = 5       # Начальная скорость
g = 9.81     # Ускорение свободного падения
t = 0.6      # Время

В Python выражения вида известны как операторы
присваивания. Значение правой части, в нашем случае целое число
, становится объектом, а имя переменной слева *— именованной
ссылкой на этот объект. Всякий раз, когда мы запишем , Python
заменит ее целым значением . Выражение создает новое
имя для того же целого объекта со значением , а не копирует
объект.

Таким образом, прочитав эти строки интерпретатор Python знает три
переменных и их значения. Эти переменные используются
интерпретатором в следующей строке, фактически реализующей некоторую
формулу

y = v0*t - 0.5*g*t**2

В этой строке Python интерпретирует как оператор умножения, *—
вычитания, *— возведения в степень (естественно, и
интерпретируются как операторы сложения и деления соответственно). В
результате вычисляется значение по формуле в правой части выражения,
которое присваивается переменной с именем . Последняя строка
сценария

print y

выводит на печать значение переменной . Таким образом при запуске
сценария ball.by на экране будет выведено
число . В тексте сценария имеются также и пустые строки, которые
пропускаются интерпретатором Python. Они добавлены для лучшей
читабельности кода.

Запуск сценариев Python

Сценарии Python обычно имеют расширение , но это не является
необходимым. Как мы уже говорили, рассмотренный выше сценарий сохранен
в файле ball.py. Запустить его можно
следующей командой:

python ball.py

Такая команда явно указывает, что в качестве интерпретатора файла
должен использоваться Python. Также могут задаваться
аргументы командной строки, который загружается сценарием.

Команда должна запускаться в консольном окне
(терминал в Unix, Командная строка (Command Prompt) в MS Windows).

В случае, когда файлу установлено разрешение на выполнение (команда
) в ОС Unix (Linux), сценарий можно запускать
командой, сценарий можно запускать командой

./ball.py

В этом случае первая строка сценария должна содержать описание
интерпретатора:

#!/usr/bin/env python

В ОС MS Windows можно писать просто

ball.py

вместо , если расширение ассоциировано с
интерпретатором Python.

Вычисление квадратного корня в Python с помощью модуля cmath

Модуль cmath используется для вычисления квадратного корня в python из Действительного или сложного числа.

Вышеприведенные два метода прекрасно работают для всех положительных вещественных чисел. Но для отрицательных или комплексных чисел это можно сделать следующим образом.

<Пример: Вычисление квадратного корня из числа с помощью math

Выход:

В этой программе мы используем функцию sqrt() в href=”https://docs.python.org/2/library/cmath.html”>cmath (комплексная математика) модуль

Обратите внимание, что мы также использовали функцию eval() вместо float() для преобразования комплексного числа. Кроме того, обратите внимание на то, как форматируются выходные данные

href=”https://docs.python.org/2/library/cmath.html”>cmath (комплексная математика) модуль. Обратите внимание, что мы также использовали функцию eval() вместо float() для преобразования комплексного числа. Кроме того, обратите внимание на то, как форматируются выходные данные.

Базовые структуры данных Python

К ним относятся:

Целые числа

Над ними можно производить операции сложения (a + b), вычитания (a — b), деления (a / b) – в этом случае результат может стать вещественным если не делится нацело, умножения (a * b). Есть операция остаток от деления (a % b), например, если разделить 5 на 2 (5 % 2 = 1), то остаток от деления будет 1.

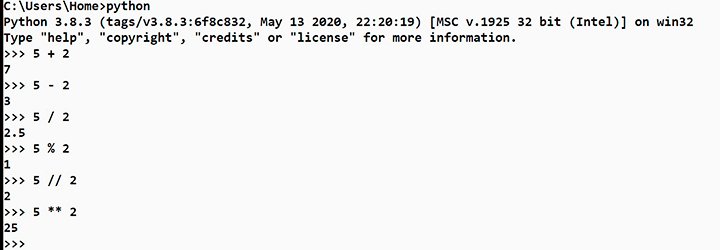
Остаток от деления записывается при помощи знака процент %. При помощи двойного слэша ( // ) можно выполнить деление нацело, при этом отбрасывается дробная часть. Например, если разделить нацело 5 на 2, то мы получим 2 (5 // 2 = 2), остаток 1 не будет учитываться.

Числа можно сравнивать. Для этого используются сравнения больше ( > ), меньше ( < ), больше или равно ( >= ), меньше или равно ( <= ), равенства ( == ) – записывается как двойное равенство, не равно ( != ) – записывается как восклицательный знак и равно. Результатом выполнения этих операций является истина или ложь (True) или (False).

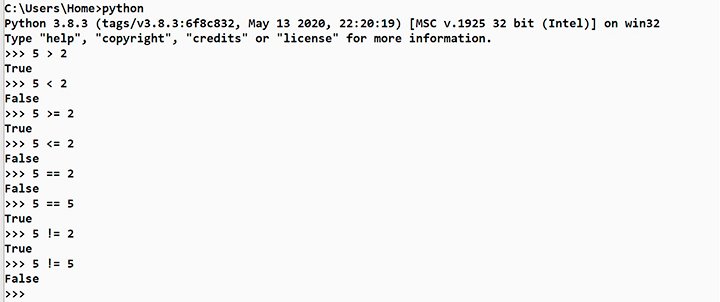
Также можно делать тройное сравнение, например, (2 < 4 < 6)  будет «True» — истина, (5 < 2 < 7) даст результат ложь «False». При помощи тройного сравнения можно проверить попадает ли в нужный диапазон

Вещественные типы данных

Это числа с дробной частью или еще они называются с плавающей точкой. Над ним можно производить все действия применимые к целым. Но операции над вещественными числами происходят с округлением, что может привести к ошибкам. Если сложить (0,3 + 0,3 + 0,3 +0,1), то получим 0.9999999999999999.

Для более точных вычислений в языке Python существуют числа с заданной точностью. Все операции между числами с плавающей точкой дают вещественные величины, между вещественным и целым также являются вещественными.

Можно возводить в дробную степень, что фактически является извлечением корня. Вещественное число можно конвертировать в целое ( int(41.3) = 41), а целое можно привести к вещественному ( float(41) = 41.0 ).

Для числовых данных приоритетным является выражение, заключенное в скобки. Далее по приоритетам идет возведение в степень, затем умножение и деление, сложение и вычитание, унарный минус.

Булевы значения

К ним применимы операции булевой алгебры. К ним относятся:

—  Логическое сложение – дизъюнкция («или» — на английском языке «or»). В этом случае если есть хотя бы одно «True», то выражение будет истинно

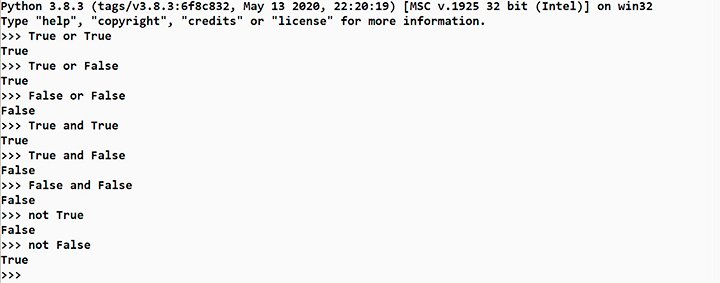
— Логическое умножение – конъюнкция («и» — «and»). Выражение истинно, когда все его элементы одинаковы.

— Логическое отрицание – инверсия («не» — «not»). Отрицание меняет истину на ложь, а ложь на истину.

Логические операции с десятичным модулем

Decimal содержит набор встроенных функций для выполнения логических операций с десятичными числами, таких как AND, OR, XOR и т. Д.

• Функция logical_and(): выполняет операцию логического И над двумя десятичными числами и возвращает результат.
• Функция logical_or(): выполняет операцию логического ИЛИ над двумя десятичными числами и возвращает результат.
• Функция logical_xor(): выполняет логическую операцию XOR над двумя десятичными числами и возвращает результат.

#Syntax for logical_and() function-
decimal1.logical_and(decimal2)

#Syntax for logical_or() function-
decimal1.logical_or(decimal2)

#Syntax for logical_xor() function-
decimal1.logical_xor(decimal2)

Пример:

import decimal as d

valx = d.Decimal(1001)
valy = d.Decimal(1111)

print("Value 1: ",valx)
print("Value 2: ",valy)

AND = valx.logical_and(valy)
print("The logical AND value of the two decimals: ",AND)

OR = valx.logical_or(valy)
print("The logical OR value of the two decimals: ",OR)

XOR = valx.logical_xor(valy)
print("The logical XOR value of the two decimals: ",XOR)

Выход:

Value 1:  1001
Value 2:  1111
The logical AND value of the two decimals:  1001
The logical OR value of the two decimals:  1111
The logical XOR value of the two decimals:  110

Тригонометрические функции в Python

Модуль math в Python поддерживает все тригонометрические функции. Самые популярные представлены ниже:

• : Возвращает синус в радианах;
• : Возвращает косинус в радианах;
• : Возвращает тангенс в радианах;
• : Возвращает инвертированный синус. Аналогичным образом работают и ;
• : Конвертирует угол из радиан в градусы;
• : Конвертирует угол из градусов в радианы.

Рассмотрим следующий пример:

Python

import math

angle_In_Degrees = 62
angle_In_Radians = math.radians(angle_In_Degrees)

print(‘Значение угла:’, angle_In_Radians)
print(‘sin(x) равен:’, math.sin(angle_In_Radians))
print(‘tan(x) равен:’, math.tan(angle_In_Radians))
print(‘cos(x) равен:’, math.cos(angle_In_Radians))

Вывод

Shell

Значение угла: 1.0821041362364843
sin(x) равен: 0.8829475928589269
tan(x) равен: 1.8807264653463318
cos(x) равен: 0.46947156278589086

Обратите внимание, что вначале мы конвертировали значение угла из градусов в радианы для осуществления дальнейших операций

Функция экспоненты exp() в Python

Библиотека Math в Python поставляется с функцией , которую можно использовать для вычисления значения . К примеру, — экспонента от . Значение равно .

Метод может быть использован со следующим синтаксисом:

Python

math.exp(x)

Параметр может быть положительным или отрицательным числом. Если не число, метод возвращает ошибку. Рассмотрим пример использования данного метода:

Python

import math

# Инициализация значений
an_int = 6
a_neg_int = -8
a_float = 2.00

# Передача значений методу exp() и вывод
print(math.exp(an_int))
print(math.exp(a_neg_int))
print(math.exp(a_float))

Вывод

Shell

403.4287934927351
0.00033546262790251185
7.38905609893065

Мы объявили три переменные и присвоили им значения с различными числовыми типами данных. Мы передали значения методу для вычисления их экспоненты.

Мы также можем применить данный метод для встроенных констант, что продемонстрировано ниже:

Python

import math

print(math.exp(math.e))
print(math.exp(math.pi))

Вывод

Shell

15.154262241479262
23.140692632779267

При передаче не числового значения методу будет сгенерирована , как показано далее:

Python

import math

print(math.exp(«20»))

Вывод

Shell

Traceback (most recent call last):
File «C:/Users/admin/mathe.py», line 3, in <module>
print (math.exp(«20»))
TypeError: a float is required

Как видно из примера выше, генерируется ошибка .

Интерактивное программирование[править]

Особенно удобная возможность, предоставляемая Python — это возможность быстро проверить как работают инструкции или выражения в интерактивном режиме. Такие интерактивные оболочки называются shell. Мы уже пользовались ей как частью IDLE. Остановимся сейчас на ней поподробнее.

Interactive Shellправить

Программа, с которой мы работали в первом уроке, может быть напечатана строчка за строчкой с тем же конечным результатом:

>>> v0 = 5
>>> g = 9.81
>>> t = 0.6
>>> y = v0 * t - 0.5 * g * t ** 2
>>> print (y)
1.2342

Мы можем легко задать новое значение переменной, например для v0, и всегда способны проконтролировать, что новое значение присвоено, введя имя переменной напрямую или через инструкцию print::

>>> v0 = 6
>>> v0
6
>>> print (v0)
6

Следующий шаг — обновить выражения, в которых еще содержится старое значение, то есть нашу формулу для y. В таком редакторе как IPython можно найти предыдущее выражение, с помощью кнопок со стрелками. О возможностях этого редактора мы еще поговорим. А пока:

>>> y = v0 * t - 0.5 * g * t ** 2
>>> y
1.8341999999999996
>>> print (y)
1.8342

Причина, по которой мы получили сейчас два разных результата, в том, что, если вы просто пишите y, то вы увидите все знаки после точки, находящиеся в памяти компьютера (16), в то время как инструкция print ограничивает число знаков и, таким образом, дает ответ с достаточной точностью. Впрочем, в некоторых версиях Python автоматически округляет значение переменной.

Преобразование типаправить

Если вы ранее работали с другими языками программирования, то могли заметить, что мы пишем программы не заботясь о задании типов переменных (вернее даже типов объектов, на которые ссылаются переменные). Однако в этом уроке мы встретились с вопросом типов объектов, когда изучали ошибку целочисленного деления, которая научила нас более внимательно относиться к типам объектов. Следующий пример иллюстрирует функцию type( ) и то, как мы можем изменять тип объекта. Для начала, создадим объект типа int, на который будет ссылаться имя С:

>>> C = 21
>>> type(C)
<type 'int'>

Теперь мы преобразуем наш объект С типа int к соответствующему объекту типа float:

>>> C = float(C)     #  type  conversion
>>> type(C)
<type 'float'>
>>> C
21.0

В инструкции C = float(C) мы создали новый объект из оригинального объекта с тем же именем. Теперь имя С ссылается на новый объект. Изначальный объект типа int со значением 21 теперь недоступен, поскольку у него больше нет имени и автоматически удаляется из памяти.

Мы также можем сделать и обратное, то есть конвертировать объект типа float к объекту типа int:

>>> C = 20.9
>>> type(C)
<type 'float'>
>>> D = int(C) #  type  conversion
>>> type(D)
<type 'int'>
>>> D
20  # decimals  are  truncated  :-/

Как и следовало ожидать, переход к целым числам отрезал дробную часть. Если вас это не устраивает, и вам требуется округление до ближайшего целого, то существует простая функция:

>>> round(20.9)
21.0
>>> int(round(20.9))
21

Типы данных и преобразование типов

Перечислим основные типы данных в Python, которые понадобятся на ближайших уроках:

• int – целочисленные значения;float – вещественные (дробные) значения;bool – логические значения — истина (True) или ложь (False);str – символьная строка или единичный символ.

Рассмотрим примеры использования основных типов в Python:Целые числа (int):

num = 13
print(num)  # 13
 
num = 
print(num)  # 0
 
num = -10
print(num)  # -10
 
num = 500_000_000  # для удобства чтения
print(num) # 500000000

Вещественные числа (float):

num = 13.4
print(num) # 13.4
 
num = 0.0
print(num) # 0.0
 
num = -15.2
print(num) # -15.2
 
num = 100_000.000_002 # для удобства чтения
print(num) # 100000.000002
 
num = 1.7e2 # 1.7 умножить на 10 в степени 2
print(num) # 170

Логический тип (bool):

print(15 == 15) # True
 
print(1 != 3) # True
 
print(3 > 4) # False
 
print(3 <= 3) # True
 
print(6 >= 6) # True
 
print(6 < 5) # False
 
x = 2
print(1 < x < 3) # True

Строки (str):

example_string = "Очень интересно"
print(example_string) # Очень интересно
 
example_string = 'Пьеса "На дне"'
print(example_string) # Пьеса "На дне"
 
example_string = "Пьеса \"На дне\"
print(example_string) # Пьеса "На дне"
 
example_string = "Как " \
                 "разбить " \
                 "объявление длинной строки"
print(example_string) # Как разбить объявление длинной строки
 
example_string = """
                 Как  
                 оставить сроку
                 в несколько строк
                 """
print(example_string) 
# Как  
# оставить сроку
# в несколько строк

# Как объединить две строки в одну
print("Можно их" + " сложить") # Можно их сложить 
 
print("Можно и так!" * 3) # Можно и так!Можно и так!Можно и так!

Рассмотрим примеры того, как используется преобразование типов в Питон:

• преобразование в символьную строку:

1
2
3

a = 1.7
a=str(a)
print(a) # '1.7'

преобразование в целое:

1
2
3

x = 1.7
x=int(x)
print(x) # 1

преобразование в вещественное:

1
2
3

y=1
y=float(y)
print(y) # 1.0

Программа на Python, использующая библиотечные функции

Представим, мы стоим на расстоянии, например, 10 м, и наблюдаете за
тем как мяч поднимается в воздух после броска. Прямая соединяющая нас
и мяч составляет некий угол с горизонтальной прямой, величина которого
возрастает и убывает, когда мяч поднимается и опускается
соответственно. Давайте рассмотрим положение мяча в некоторый момент
времени, когда высота положения мяча равна 10 м.

Вычислим рассматриваемый нами угол. Перед тем как написать программу,
мы должны сформулировать некий алгоритм, т.е. некий способ
выполнения необходимых вычислений. В нашем случае, пусть \( x \) —
расстояние от нас до точки подброса мяча, а \( y \) — высота, на
которой находится мяч. Таким образом, образуется угол \( \theta \) с
поверхностью земли, где \( \mathrm{tg\,} \theta = y/x \). Следовательно,
\( \theta=\mathrm{arctg\,}(y/x) \).

Напишем сценарий выполняющий эти вычисления. Введем переменные и
для координат положения \( x \) и \( y \), и переменную
для угла \( \theta \). Сценарий сохраним в файл
ball_angle.py

# -*- coding: utf-8 -*-

x = 10   # горизонтальное положение
y = 10   # вертикальное положение

angle = atan(yx)

print (anglepi)*180

В этом сценарии строка иллюстрирует
вызов функции , соответствующей математической функции
\( \mathrm{arctg} \), с выражением в качестве аргумента
или входного параметра. Отметим, что тригонометрические функции
(такие как ) возвращают значение угла в радианах, поэтому для
преобразования результата в градусы мы использовали выражение
.

Теперь, запустив на выполнение сценарий, мы получим ошибку

NameError: name 'atan' is not defined

Очевидно, интерпретатор Python не распознал функцию , так как
эта функция еще не импортирована в программу. Достаточно большой
функционал доступен в интерпретаторе по умолчанию, однако намного
больший функционал реализован в библиотеках Python. Для того, чтобы
активировать использование дополнительного функционала, мы должны его
явно импортировать. В Python функция , как и множество других
математических функций, собраны в библиотеке . Такая
библиотека в терминах Python называется модулем. Чтобы мы могли
использовать функцию в нашем сценарии, мы должны написать

from math import atan

Добавив данную строку в начало сценария и запустив его, мы приходим к
другой проблеме: переменная не определена. Переменная ,
соответствующая значению \( \pi \), также определена в модуле , и
тоже должна быть импортирована

from math import atan, pi

Очевидно, что достаточно сложно импортировать поименно все необходимые
нам функции и переменные из модуля , поэтому существует
быстрый способ импортировать все из модуля :

from math import *

Мы будем использовать такое выражение для импорта, чтобы иметь доступ
ко всем общим математическим функциям. Таким образом рабочий сценарий
ball_angle.py имеет вид:

# -*- coding: utf-8 -*-
from math import *

x = 10   # горизонтальное положение
y = 10   # вертикальное положение

angle = atan(yx)

print (anglepi)*180

На первый взгляд кажется громоздким использование библиотек, так как
мы должны знать какой модуль импортировать, чтобы получить желаемый
функционал. Возможно, более удобно иметь доступ ко всему необходимому
в любое время. Однако это означает, что мы заполним память программы
большим количеством информации, которую мы будем редко использовать
для вычислений. Поэтому Python имеет большое количество библиотек,
реализующих огромные возможности, из которых мы можем импортировать
только необходимые в данный момент.

Вычисление квадратного корня в Python С помощью функции sqrt()

Математический модуль Python имеет дело с математическими функциями и вычислениями. Функция sqrt() в математическом модуле используется для вычисления квадратного корня из заданного числа.

Возвращаемое значение функции sqrt()

метод sqrt() в Python вернет квадратный корень из заданного числа с плавающей запятой. Если значение меньше 0, то он вернет ошибку времени выполнения.

Примеры Вычисления Квадратного Корня С Помощью Функции sqrt()

Давайте рассмотрим несколько примеров вычисления квадратного корня Python с помощью функции sqrt ().

Пример 1: Вычисление квадратного корня из положительного целого числа

Выход:

Пример 2: Вычисление квадратного корня из числа с плавающей запятой

Выход:

Пример 3: Вычисление квадратного корня из 0

Выход:

Выход:

Выход:

Таким образом, когда x <0 он не выполняется, вместо этого генерируется ValueError.

Пример 5: Вычисление квадратного корня из постоянной Больцмана

Выход:

Записи:

• функция math.sqrt () – это встроенная функция в языке программирования Python, которая предоставляет квадратный корень из заданного числа. Для работы функции math.sqrt() необходимо импортировать модуль (библиотеку) “math”. Если вы передадите отрицательное значение в функцию sqrt, то python выдаст ошибку

Встроенные структуры данных Python

Списки – создаются при помощи квадратных скобок . В списках находятся значения, которые можно изменять. Это могут быть любые значения: числа, символы, строки и т.д. Также можно создать список при помощи функции list( ).

Словари – формируются при помощи фигурных скобок { } или функцией dict( ). Являются изменяемым объектом и включают себя попарно набор ключей и значений.   

Кортежи – инициализируются при помощи обычных скобок ( ), еще можно использовать функцию tuple( ). Их можно назвать неизменяемым списком. После создания кортежа нельзя изменять его значения.

Множество – создание происходит с использованием фигурных скобок, как и в случае со словарем или применив функцию set( ). Множество содержит элементы, которые не повторяются и находятся в случайном порядке. Пустое множество создать нельзя. Множество удобно применять для того, чтобы удалить повторяющиеся элементы.

Кубический корень

Само название функции намекает нам на то, что она не подходит для извлечения корня степени отличной от двойки. Поэтому для извлечения кубических корней, сначала необходимо вспомнить связь между степенями и корнями, которую продемонстрируем на корне квадратном:

Вышеуказанное соотношение несложно доказать и для других степеней вида .

В случае с квадратным или кубическим корнем эти операции действительно эквивалентны, но, вообще говоря, в математике извлечение корня и возведение в дробную степень имеют существенные отличия при рациональных степенях вида m/n, где m != 1. Формально, в дробно-рациональную степень можно возводить только положительные вещественные числа. В противном случае возникают проблемы:

Таким образом, извлечь кубический корень в Python можно следующим образом:

Или же:

Транспонирование матрицы

Транспонирование матрицы в основном включает в себя переворачивание матрицы по соответствующим диагоналям, т. е. Меняет местами строки и столбцы входной матрицы. Строки становятся столбцами и наоборот.

Например: давайте рассмотрим матрицу A с размерами 3 × 2, т.е. 3 строки и 2 столбца. После выполнения операции транспонирования размеры матрицы A будут 2 × 3, т.е. 2 строки и 3 столбца.

основном выполняет транспонирование входной матрицы и создает новую в результате операции транспонирования.

Пример:

import numpy
 
matA = numpy.array()
print("Original Matrix A:\n")
print(matA)
print('\nDimensions of the original MatrixA: ',matA.shape)
print("\nTranspose of Matrix A:\n ")
res = matA.T
print(res)
print('\nDimensions of the Matrix A after performing the Transpose Operation:  ',res.shape)

Выход:

Original Matrix A:


 ]

Dimensions of the original MatrixA: (2, 5)

Transpose of Matrix A:
 

 
 
 
 ]

Dimensions of the Matrix A after performing the Transpose Operation: (5, 2)

В приведенном выше фрагменте кода я создал матрицу размером 2 × 5, т.е. 2 строки и 5 столбцов.

После выполнения операции транспонирования размеры результирующей матрицы составляют 5 × 2, то есть 5 строк и 2 столбца.

Деление с остатком Python

Оператор % используется для деления по модулю, и возвращает остаток от деления, а не частное. Это полезно, например, для нахождения множителей числа.

Деление по модулю Python (с остатком) — пример:

o = 85
p = 15
print(o % p)

Вывод

10

В этом примере 85 делится на 15. Результат – 5 с остатком 10. Значение  выводится, поскольку оператор возвращает остаток от деления.

Если мы используем два числа с плавающей точкой для деления по модулю, число с плавающей точкой будет возвращено в качестве остатка:

q = 36.0
r = 6.0
print(o % p)

Вывод

0.0

В приведенном выше примере 36.0 делится на 6.0 без остатка, поэтому возвращается значение 0.0.

Функция exp() — вычисление экспоненты

Функция вычисляет значение экспоненты, то есть e ^ x конкретного числа переданной десятичной точки.

Синтаксис:

decimal.Decimal(decimal-number).exp()

Пример:

import decimal as d

d.getcontext().prec = 5

#Intializing with an addition operation
val = d.Decimal(12.201) + d.Decimal(12.20)

#Calculating exponential of the decimal value
exp = val.exp()

#variable with no calculations
no_math = d.Decimal(1.131231)

print("Sum: ",val)
print("Exponential: ", exp)
print(no_math)

Выход:

Decimal Number:  24.401                                                                                                       
3.9557E+10                                                                                                                    
1.131231000000000097571728474576957523822784423828125   

Следует помнить, что значение точности применяется, когда вы выполняете математические операции с двумя десятичными знаками, а не когда вы напрямую инициируете переменную со значениями, как показано с переменной «no_math» выше.

Отрицательные значения и ноль

Функция sqrt в «Питоне» — вещь полезная и знать ее нужно, однако она не принимает отрицательного числа — лишь положительные (целые и вещественные), а также ноль.

Такая ограниченная возможность использования не соответствует математическим канонам, ведь в реальной жизни специалисты по математике без проблем извлекают √ и из отрицательных значений. Да, результат будет комплексным и пригодится лишь для решения довольно узкого спектра задач, типа расчетов волновых явлений в физике либо вычислений в энергетической сфере.

Учитывайте вышесказанное, если пытаетесь извлекать корни в Python посредством этой функции. Передав отрицательное значение, вы получите error:

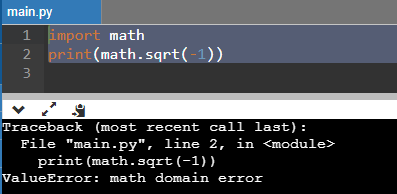
А вот если говорить про ноль, то ошибки не будет, так как код отработает корректно. Однако результат тут очевиден, поэтому практическая ценность данной возможности весьма условна:

Хотите знать о «Питоне» намного больше? Добро пожаловать на специализированный курс в «Отус»!

По материалам:

9 ответов

Лучший ответ

Это самое простое и наиболее питонное решение, которое я могу придумать:

Если входные данные очень большие, то решение итераторов должно быть более удобным:

И, конечно же, очень, очень ленивое решение для парней (если вы не против получить массивы вместо списков, но в любом случае вы всегда можете вернуть их в списки):

51

fortran
29 Июл 2009 в 16:10

Множественное число индекса — это индексы. Идем для простоты / читабельности.

-1

anthony
29 Июл 2009 в 07:56

Вот еще один ответ.

Поддерживает отрицательные показатели и тому подобное.

Steve Losh
29 Июл 2009 в 16:31

2

anthony
30 Сен 2009 в 20:26

Это все, что я мог придумать

Il-Bhima
29 Июл 2009 в 08:18

Мое решение похоже на решение Il-Bhima.

Альтернативный подход

Если вы хотите немного изменить способ ввода индексов, с абсолютных индексов на относительные (то есть с на , то нижеприведенное также даст вам желаемый результат, хотя это не так. создать списки посредников.

7

Cide
29 Июл 2009 в 10:11

Мне было бы интересно увидеть более Pythonic способ сделать это также. Но это дерьмовое решение. Вам необходимо добавить проверку для пустого списка индексов.

Что-то вроде:

Производит

9

john gonidelis
17 Дек 2018 в 14:02

Maxima mea culpa: он использует оператор , и он не использует такие штуковины, как itertools, zip (), None в качестве стража, списки, …

😉

5

John Machin
30 Июл 2009 в 03:32

Cide’s создает три копии массива: + копии индексов, ( + индексы) + [] копии снова, а индексы будут копироваться в третий раз. Ил-Бхима делает пять экземпляров. (Я не считаю возвращаемое значение, конечно.)

Их можно уменьшить (izip, islice), но вот версия с нулевой копией:

Конечно, копии массивов довольно дешевы (нативный код) по сравнению с интерпретируемым Python, но у этого есть еще одно преимущество: его легко использовать повторно и напрямую изменять данные:

(Вот почему я передал индексы в iterate_pairs. Если вас это не волнует, вы можете удалить этот параметр и просто сделать так, чтобы в последней строке было указано «yield prev, None», а это все, что нужно для partition ().)

Glenn Maynard
29 Июл 2009 в 08:20

Связь с другими языками

pythonnet

Иногда возникает потребность запустить код, написанный на другом языке, через Python, например, в целях проверки работы какого-либо стороннего модуля или для оптимизации кода. Существует несколько библиотек, позволяющих сделать это, например, pythonnet позволяет запустить некоторую часть кода, написанную на C# в Python (pythonnet позволяет рассматривать множество элементов clr, как модули в python).

Создаем проект библиотеки классов C# в visual studio, создаем в неё нужный класс или методы (в случае примера класс, содержащий метод вычисления дискриминанта), создаем .dll и запускаем через pythonnet (более подробно тут):

Обращаемся к C# через Python

JPype

Для этих же целей существует библиотека, которая позволяет запустить Java код в Python. Эта библиотека называется — JPype. Рассмотрим пример работы библиотеки.

Для начала установим её pip install jpype1, далее создадим Java проект, который в будущем скомпилируем в .jar архив, в проекте необходимо создать пакет, в нём класс и прописать следующий код (код вычисляет объем цилиндра):

Теперь можно создать .jar решение проекта.

В python коде импортируем библиотеку jpype, запустим JVM и пропишем путь к созданному .jar архиву. Далее по аналогии с pythonnet импортируем необходимые пакеты и классы:

Таким образом, pythonnet и jpype — отличные решения для интеграции кода C# и Java в  Python проект.

Вывод данных. Функция print()

Что такое функция в программировании, узнаем позже. Пока будем считать, что – это такая команда языка Python, которая выводит то, что в ее скобках на экран.

>>> print(1032)
1032
>>> print(2.34)
2.34
>>> print("Hello")
Hello

В скобках могут быть любые типы данных. Кроме того, количество данных может быть различным:

>>> print("a:", 1)
a: 1
>>> one = 1
>>> two = 2
>>> three = 3
>>> print(one, two, three)
1 2 3

Можно передавать в функцию как непосредственно литералы (в данном случае «a:» и 1), так и переменные, вместо которых будут выведены их значения. Аргументы функции (то, что в скобках), разделяются между собой запятыми. В выводе вместо запятых значения разделены пробелом.

Если в скобках стоит выражение, то сначала оно выполняется, после чего уже выводит результат данного выражения:

>>> print("hello" + " " + "world")
hello world
>>> print(10 - 2.5/2)
8.75

В предусмотрены дополнительные параметры. Например, через параметр можно указать отличный от пробела разделитель строк:

>>> print("Mon", "Tue", "Wed", "Thu",
... "Fri", "Sat", "Sun", sep="-")
Mon-Tue-Wed-Thu-Fri-Sat-Sun
>>> print(1, 2, 3, sep="//")
1//2//3

Параметр позволяет указывать, что делать, после вывода строки. По-умолчанию происходит переход на новую строку. Однако это действие можно отменить, указав любой другой символ или строку:

>>> print(10, end="")
10>>>

Обычно используется не в интерактивном режиме, а в скриптах, когда несколько выводов подряд надо разделить не переходом на новую строку, а, скажем, запятыми. Сам переход на новую строку обозначается символом ‘\n’. Если присвоить это значение параметру , то никаких изменений в работе функции вы не увидите, так как это значение и так присвоено по-умолчанию:

>>> print(10, end='\n')
10
>>>

Однако, если надо отступить на одну дополнительную строку после вывода, то можно сделать так:

>>> print(10, end='\n\n')
10

>>>

Следующее, что стоит рассказать о функции – это использование форматирования строк. На самом деле оно никакого отношения к не имеет, а применяется к строкам. Однако часто форматирование используется в сочетании с вызовом функции .

Форматирование может выполняться в так называемом старом стиле или с помощью строкового метода . Старый стиль также называют Си-стилем, так как он схож с тем, как происходит вывод на экран в языке C. Рассмотрим пример:

>>> pupil = "Ben"
>>> old = 16
>>> grade = 9.2
>>> print("It's %s, %d. Level: %f" %
... (pupil, old, grade))
It's Ben, 16. Level: 9.200000

Здесь вместо трех комбинаций символов , , подставляются значения переменных pupil, old, grade. Буквы , , обозначают типы данных – строку, целое число, вещественное число. Если бы требовалось подставить три строки, то во всех случаях использовалось бы сочетание .

Хотя в качестве значения переменной grade было указано число 9.2, на экран оно вывелось с дополнительными нулями. Однако мы можем указать, сколько требуется знаков после запятой, записав перед буквой точку с желаемым числом знаков в дробной части:

>>> print("It's %s, %d. Level: %.1f"
...  % (pupil, old, grade))
It's Ben, 16. Level: 9.2

Теперь посмотрим на метод :

>>> print("This is a {0}. It's {1}."
... .format("ball", "red"))
This is a ball. It's red.
>>> print("This is a {0}. It's {1}."
... .format("cat", "white"))
This is a cat. It's white.
>>> print("This is a {0}. It's {1} {2}."
... .format(1, "a", "number"))
This is a 1. It's a number.

В строке в фигурных скобках указаны номера данных, которые будут сюда подставлены. Далее к строке применяется метод . В его скобках указываются сами данные (можно использовать переменные). На нулевое место подставится первый аргумент метода , на место с номером 1 – второй и т. д.

На самом деле возможности метода существенно шире, и для их изучения понадобился бы отдельный урок. Нам пока будет достаточно этого.